P10678 『STA - R6』月 题解
Solution
看了别的大佬的题解,感觉都是数学证明然后用树和图做的,看不懂啊。。。萌新瑟瑟发抖
用 vector 模拟树,然后贪心摸索做出来了。注意到要求最深叶子结点和最浅叶子结点的距离最短时的情况,那么此时根节点应该是树中度数最大的点,把树尽可能的拓宽,深度换宽度。
那么同理的根节点的子树的根节点应该也是该子树中度数最深的点,那么可得出该树应该是类似一个大根堆(出度不一定为 \(2\),因此类似),且每层的数量其实是固定的(由上一层的度数之和决定,而根节点又确定),因此仅通过一次排序,便可得到由根节点到最后一个叶子结点,每层的顺序:
如:样例第四
7
1 3 2 3 1 1 1
通过结构体将每个元素的度数和原次序绑定,得如下顺序:
(后期要改度数用出度,将除了根节点之外的度数均减一)
//表格一
4
2
1 1
&&&
1 2 //原次序
1 1 //度数
&&&
3
1 1 2
&&&
3 1 2
2 1 1
&&&
5
1 1 2 2 2
&&&
3 4 5 1 2
2 2 2 1 1
&&&
7
1 3 2 3 1 1 1
&&&
2 4 3 1 5 6 7
3 3 2 1 1 1 1
&&&
然后再将 "&&" 中的结构体装进 vector 里面模拟树(仅是因为 vector 方便打,其实用树结构体存效果一样):
//表格二
4
2
1 1
&&&1 &&& //树中存的是节点的次序
&&&2 &&&
&&&1 &&& //树中存的是节点的出度
&&&0 &&&
3
1 1 2
&&&3 &&&
&&&1 2 &&&
&&&2 &&&
&&&0 0 &&&
5
1 1 2 2 2
&&&3 &&&
&&&4 5 &&&
&&&1 2 &&&
&&&2 &&&
&&&1 1 &&&
&&&0 0 &&&
7
1 3 2 3 1 1 1
&&&2 &&&
&&&4 3 1 &&&
&&&5 6 7 &&&
&&&3 &&&
&&&2 1 0 &&&
&&&0 0 0 &&&
“&”“&” 中的是 vector 数组中每层的情况,(除了根节点之外的节点度数减了 \(1\),转变成出度)。而决定该层数是由上一层的所有点的出度之和(第二层根据根节点的出度)。下一层中的任何一个都可做上一层节点的孩子,不影响树的最深最浅叶子结点层数。
最后把树的情况输出来即可:
如最后一例:
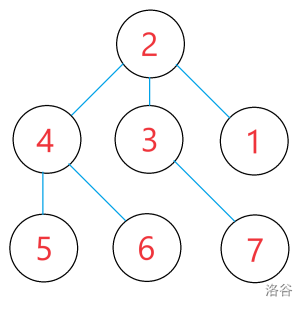
&&&2 &&& //节点次序
&&&4 3 1 &&&
&&&5 6 7 &&&
&&&3 &&& //3->2,3->1,3->0
&&&2 1 0 &&& //2->0,2->0,2->0
&&&0 0 0 &&& //父节点领养子节点情况
//将上面的诸如 \(2\),\(0\) 之类转成\(↑\)上面树中存的节点次序输出来即可变成:
Code
#include <bits/stdc++.h>
using namespace std;
#define to(x,y); for(int x=1;x<=y;x++)
#define fr(x,y); for(int x=0;x<y;x++)
const int N = 2e5 + 20;
int t, n, sum[N];
struct nd {
int ord, cry;
} p[N];
vector<nd> tr[N];
bool cmp(nd a, nd b) {
if (a.cry == b.cry)
return a.ord < b.ord;
return a.cry > b.cry;
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
to(i, n)scanf("%d", &p[i].cry), p[i].ord = i;
sort(p + 1, p + 1 + n, cmp);
to(i, n) {
if (i > 1)
p[i].cry--;
sum[i] = sum[i - 1] + p[i].cry;
}
int l = 1, r = 1, num, dep = 1;
tr[1].push_back({p[1].ord, p[1].cry});
while (r < n) {
dep++;
num = sum[r] - sum[l - 1];
l = r + 1, r = r + num;
for (int i = l; i <= r; i++)
tr[dep].push_back({p[i].ord, p[i].cry});
}
to(i, dep - 1) {
int len = tr[i].size(), idx = 0;
fr(j, len) {
for (int k = 0; k < tr[i][j].cry; k++) {
printf("%d %d\n", tr[i][j].ord, tr[i + 1][idx + k]);
}
idx += tr[i][j].cry;
}
}
to(i, dep)vector <nd>().swap(tr[i]);
}
return 0;
}
附带表格可视化并附解释
#include <bits/stdc++.h>
using namespace std;
#define to(x,y); for(int x=1;x<=y;x++) //丑陋的代码化简习惯
#define fr(x,y); for(int x=0;x<y;x++)
const int N = 2e5 + 20;
int t, n, sum[N];
// sum 为出度前缀和,求每层的节点数
struct nd {
int ord, cry;
} p[N]; //存输入数据并做预处理用
vector<nd> tr[N];//核心 vector 树
bool cmp(nd a, nd b) {
if (a.cry == b.cry)
return a.ord < b.ord;
return a.cry > b.cry;
}//排序预处理
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
// memset(p, 0, sizeof p); //无用的初始化
to(i, n)scanf("%d", &p[i].cry), p[i].ord = i;
sort(p + 1, p + 1 + n, cmp);
/*表格一*/
// puts("\n&&&");
// to(i, n)printf("%d ", p[i].ord);
// puts("");
// to(i, n)printf("%d ", p[i].cry);
// puts("\n&&&\n");
to(i, n) {
if (i > 1)
p[i].cry--;//改度数为出度
sum[i] = sum[i - 1] + p[i].cry;//前缀和
}
int l = 1, r = 1, num, dep = 1;
tr[1].push_back({p[1].ord, p[1].cry});//存下根节点
while (r < n) {
dep++;//由上一层来到下一层
num = sum[r] - sum[l - 1];//上层度数之和
l = r + 1, r = r + num;
for (int i = l; i <= r; i++)//“领养”子节点
tr[dep].push_back({p[i].ord, p[i].cry});//存下该层子节点
}
/*表格二*/
// to(i, dep) {
// printf("&&&");
// int len = tr[i].size();
// fr(j, len)printf("%d ", tr[i][j].ord);
// puts("&&&");
// }
// puts("");
// to(i, dep) {
// printf("&&&");
// int len = tr[i].size();
// fr(j, len)printf("%d ", tr[i][j].cry);
// puts("&&&");
// }
to(i, dep - 1) {
int len = tr[i].size(), idx = 0;
// idx 为领养子节点的次序
fr(j, len) {
for (int k = 0; k < tr[i][j].cry; k++) {
printf("%d %d\n", tr[i][j].ord, tr[i + 1][idx + k]);
}//输出父子
idx += tr[i][j].cry;//领下一批子节点
}
}
to(i, dep)vector <nd>().swap(tr[i]);
//清空 vector 树
}
//完结撒花
return 0;
}