如果地球是空心的，会发生什么？我们怎么知道它不是空心的？

2024-06-24 11:12 由超自然现象探索官发表于 #社会

重力和固体地球

所以我们要看看空心地球，但首先我们需要停下来谈谈重力。让我们将重力建模为具有质量的物体之间的吸引力（而不是将其建模为时空曲率）。这样我们就可以计算由于其他一些小质量而产生的每单位质量的重力。这称为引力场（这是一个向量 g，单位为牛顿/千克）。

由于这个小质量而产生的引力场取决于质量值 (m) 和到该质量的距离 (r)。这是一个指向质量的向量，我们可以将其写成以下形式。

这里 G 是万有引力常数，值为 6.67 x 10^-11 N m²/kg²。另请注意，这里有一个 r 帽子。如果 r 是从质量到要求引力场的点的向量，那么 r-hat 就是单位向量，这使得整个表达式成为一个向量。是的，这很重要。

如果你有一个不是小点质量的物体怎么办？在这种情况下你如何找到引力场的值？事实是，引力遵循叠加原理。这意味着由多个小点质量引起的引力场只是每个质量产生的引力场的矢量和。因此，对于任何具有复杂形状的物体，我可以简单地通过将该物体分解成许多小质量来计算引力场。

让我们用这个想法来模拟真实地球的引力场。为了好玩，我们可以想象地球是由 1000 个小质量均匀分布在整个地球上组成的，其中每个质量是地球总质量的 1/1000。当然，这并不完全正确，因为地球中心的密度比表面的密度大，但这是正常的（相信我）。

这是代表我们地球的 5000 个质量

如果我用叠加原理求出地球表面（x轴上）的引力场，我得到：g =

如果用地球中心一个很小但质量很大的点代替整个地球会怎样？如果这个小点质量与地球的质量相同，它将产生与地球相同的引力场。事实上，任何球状均匀分布质量外部的引力场看起来与点质量的引力场完全相同。这是一个非常有用的想法。

现在我们准备好回答一些问题了。

如果我们只剩下地球外部 10% 厚的部分，会发生什么？

即使这不是一个完美的问题，但我不想问得太长。因此，想象一下地球内部的一部分被神奇地移除了。这使得地球的外部部分厚度为半径的 10%。由于地球半径为 6.37 x 10^6 米，因此地表厚度为 637 公里。

让我们用与上面相同的方法将地球分成5000个小质量。然而，这些质量只会位于地球的外部。而且，所有这些质量的总和不会是整个地球的质量，而是更小的质量。

表面附近物质的密度约为每立方米3500公斤（这里是密度图）。使用这个密度和剩余地球的体积（剩下的部分），我们得到的质量为 1.03 x 10^24 千克。是的，这比整个地球的质量大约少 20%。

现在让我们创建 5000 个点质量。看。

重新计算地球表面的引力场，我得到的值仅为 1.4 N/kg。这比我们正常的地球小得多——这是由于质量减少了。

可是等等！还有其他事情会发生。如果你在地球内部怎么办？让我们只对内部位置（但不是在中心 - 到中心的一半）进行计算。这给出了

是的，地球内部的引力场为零。你可以像超级英雄或丢失的气球一样四处走动（假设你有空气）。

如果内部没有被移除，而只是被压缩怎么办？

还有另一种方法可以使地球变得空心。只要把中间的所有东西都拿出来，然后把它挤到外面就可以了。这里的区别在于总质量没有改变。这意味着地球表面的引力场仍为9.8 N/kg。你真的无法区分空心地球和实心地球（在大多数情况下）。

美好的。那么我们怎么知道地球不是空心的呢？

这是一个很好的问题。想想我们如何了解地球以及它是实心的还是空心的，真是太疯狂了。我的意思是，仅凭表面是无法真正辨别的。你可以尝试看看里面是否是空心的 - 但即使挖 1 公里也不会让你走多远。让我们看一个有趣的实验，该实验表明地球是固态的。

在考虑地球之前，有几个重要的想法需要理解。第一个是万有引力的思想（这就是我们上面使用的）。1666年，艾萨克·牛顿提出，导致行星做圆周运动的力与导致物体落到地球上的力相同。所以，任何两个有质量的物体都会相互吸引。该力取决于距离和两个质量的值。

第二个想法是地球是球形的（而不是平的——每个不傻的人都知道）。地球不仅是球形的，而且地球的半径也是由埃拉托色尼确定的。所以每个人都知道地球的大小。

现在进行很酷的实验。它涉及悬挂在绳子上的物体和一座大山。这个想法是，铅垂线不是垂直悬挂的，而是沿着由此产生的引力场的方向悬挂。如果你把这条铅垂线放在一座大山旁边，山上的引力会把它拉向一边并导致它偏转。

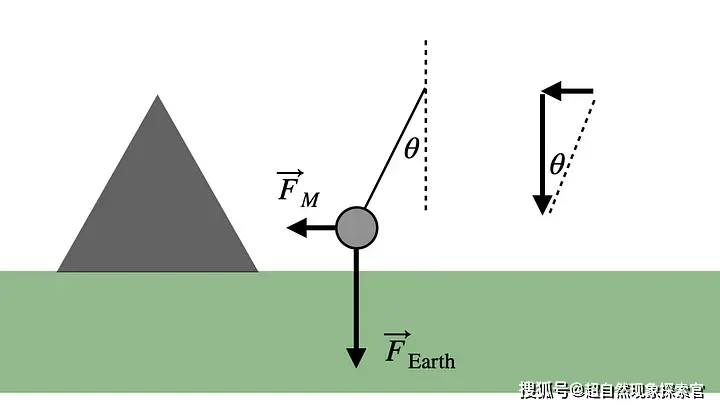
三个力作用于质量（我只显示了两个）。存在地球（向下）产生的引力、山体（侧面）产生的引力以及绳索产生的力。如果知道铅垂线的角度，就不难找到重力相对于地球力的大小。

这不是一个简单的实验。当我们通常使用铅垂线来确定垂直方向时，您可能会遇到第一个问题——如何确定铅垂线与垂直方向的偏差。安排。嗯，答案是利用星星的位置来确定垂直方向。

第二个大问题是如何找到一座山的质量？如果知道山的密度和山的体积，那么求质量就不难了。然而，确定体积确实很困难。如果您能找到一座形状正确且距离其他山脉不太近的山（这也会产生重力），这会有所帮助。

1774年，苏格兰的Schiehallion山被选中。经过仔细测量，他们发现铅垂线的偏差非常小——小于预期。根据他们假设这座山的密度为每立方米 2500 公斤，他们计算出地球的密度为 4500 公斤/立方米。注：地球的实际密度甚至更高 - 值为 5500 kg/m3。

但通过这种计算，很难假设地球内部存在任何空隙。这表明地下物质的密度非常大。更容易解释的是，地球不仅是固体（确实如此），而且也不仅仅是普通的岩石，就像行星表面那样。

卡文迪什测量引力常数 (G) 后获得了更准确的地球质量（和密度）值 - 但那是另一回事了。以下是其完成方式的预览。