1 一分钟微积分：X射线和延时视觉

我们通常只看到图形、公式和情况的表面价值。微积分为我们提供了两种深入挖掘的超能力：

• X射线

能看到图案中隐藏的部分。你不仅能看到树，还能知道它是由年轮组成的，在我们说话的同时，另一个年轮也在生长。

• 延时视觉

你能看到物体未来的运行轨迹（很酷吧？） “嘿，那是月亮。接下来几天它都会是白色的，但到了第六天，它就会出现在低空，呈现出我喜欢的颜色。到时我要拍张照片。”

微积分有什么用呢？试想一下，如果我们拥有 X 光或延时视觉，就可以随意使用了。对于我们关心的物体或场景，它是如何组合在一起的？它会发生什么变化？

1.1 微积分十分钟： 逐步查看模式

X 射线和延时视觉有什么共同点？它们都是一步一步地观察图案。X光片显示的是内部的单个切片，而延时摄影则将每个未来状态放在旁边。

这似乎很抽象。让我们来看看圆周率、面积、表面积和体积的公式：

我们隐约感觉到这些公式之间有联系，对吗？

让我们打开 X-Ray 视角，看看这会带来什么。假设我们知道
我们想计算出面积公式。我们能做什么呢？

这是个棘手的问题。正方形很容易测量，但我们如何计算出一个不断弯曲的形状的大小呢？

微积分来帮忙。让我们用 X-Ray 的视角来认识圆盘，它其实就是一堆圆环组合在一起。与树干类似，这里也是 “逐步”查看圆的面积：

这个视角有什么帮助？好吧，让我们把这些卷曲的圆环展开成直线，这样就更容易测量了：

哇哦 我们有了一堆拉直的圆环，它们组成了一个三角形，这就更容易测量了。

我们的 X 射线视野显示，在一个弯曲的形状中存在着一个简单、易于测量的结构。我们意识到，一个圆和一组粘在一起的圆环其实是一样的。从另一个角度看，一个填满的圆盘其实只是一个圆环变大的 “时间推移”。

1.2 微积分能做什么呢？

还记得学习算术吗？你学会了如何算出一个数字，以及如何将它与其他数字结合起来（加/减、乘/除、取指数/根）。从技术上讲，数数并不是必需的，因为我们的穴居祖先没有数数也能 “很好 ”地生存。

但是，有了具体的数量概念，就能更容易地驾驭世界。你没有 “大 ”和 “小 ”的石头堆：你有精确的计数。你知道每个猎人可以得到多少支箭，或者采集的浆果是否足够部落食用。

更妙的是，算术为我们提供了超越严格计算的隐喻。它使我们对万事万物的描述更加清晰，让我们明确从辛辣程度和电影评分（1 到 5）到我们的心情（1 到 10）的一切。具体的测量是一个有用的想法，而且一旦看到就很难放弃。

微积分训练了我们两种新的隐喻：拆分和粘合。一个模式可以拆分成若干部分，而这些部分又可以逐步组合成完整的模式。

这种观点是生存所必需的吗？不是。但它很有趣。

数字和方程式描述了我们所拥有的一切，而微积分则解释了我们达到目标的步骤。我们看到的不仅仅是饼干，而是配方。

当然，微积分出现在科学中，是因为一步一步的蓝图比交给我们一个最终结果更有用。但在日常场景中，我们可以打开一个很好的视角： 是哪些步骤让我们走到这里的？这种方法有什么利弊吗？根据这些步骤，我们下一步该往哪里走？

2 练习X射线和延时视觉

微积分训练我们使用 X 射线和延时视觉，例如将圆重新排列成我们在上一章中看到的 “环形三角形”。这样一来，求面积......即使算不上轻而易举，也要容易得多。

但我们还是有点冒昧了。宇宙中的每一个圆都是由环构成的吗？

当然不是 我们比那更有创造力。下面是我们可以用 X-Ray 扫描圆圈的几种方法：

我们可以把圆想象成一组圆环、披萨片或竖板。每个蓝图都是不同的分步行动策略。

2.1 逐环分析

利用“延时”视角，想象逐环策略是如何随着时间的推移不断积累的：

• 每个中间阶段本身就是一个完整的 “小圆”。也就是说，当我们完成一半时，我们仍然有一个圆，只是半径只有常规圆的一半。
• 每步的工作量都在增加。想象一下，犁一块圆形的田地，分几天来完成。第一天，你从中心开始，一动不动。第二天，你转一个最窄的弯。然后开始绕圈，越绕越大，直到最后一天绕满整个院子。
• 这项工作具有合理的可预测性，这可能有助于制定计划。如果我们知道每绕一圈要多花一分钟，那么绕第 20 圈就要花 20 分钟。
• 大部分工作都发生在最后一圈。在延时摄影的前 25%，我们几乎没有成长：我们只是在增加小环。接近尾声时，我们开始增加长环，每个环都接近最终尺寸。

一棵大树必须从一棵完整的小树生长而来。采用逐环策略，我们总是在一个完整的、完全形成的圆的基础上生长。我们并不是先种好树的 “左半边”，然后再种右边。

事实上，许多自然生长过程（树木、骨骼、气泡等）都采用这种由内而外的方法。

2.2 逐片分析

现在思考一下逐片递进的过程。你会发现什么？

• 我们每步的贡献都是一样的。更妙的是，各部分是相同的。这对数学来说可能无关紧要，但在现实生活中（例如切蛋糕），我们希望在切每一片时都使用相同的动作。
• 因为切片是对称的，所以我们可以使用捷径，比如横切整个形状。在生成完全相同的组件时，这些 “流水线”加速方法非常有效。
• 进度非常容易衡量。如果我们有 10 个切片，那么在第 6 个切片时，我们正好完成了 60%（按面积和周长计算）。
• 我们沿着一条环形路径前进，从 “角度 ”的角度来看，我们从未走回头路。在雕刻圆环时，每一步都涉及整个 360 度。

食物就是其中之一。蛋糕、披萨、馅饼：我们希望每个人都能平等分享。切片很简单，我们可以获得很好的速度（横切蛋糕），而且很容易看到剩余的数量。想象一下，从馅饼上切圆形环，然后估算还剩多少。

再想想雷达扫描仪：它们的光束扫过一圈，“清除 ”一片天空后，再移动到另一个角度。这种策略确实会在您尚未覆盖的角度留下盲点，希望您能意识到这一点。

相比之下，潜艇或蝙蝠使用的声纳会发出一个向各个方向传播的声 “环”。这对近距离目标最有效（同时覆盖各个方向）。其缺点是，由于初始能量被分散到更大的环上，因此越远的地方，非聚焦传播就越弱。我们使用扩音器和天线将信号聚焦成波束（薄片），以获得最大范围的能量。

从逻辑上讲，如果我们要从一组薄片（就像纸扇的折叠部分）中构建一个圆形，那么每个部分都完全相同会很有帮助。找出制作单个切片的最佳方法，然后批量生产。更妙的是：如果一个部分可以折叠，那么整个形状就可以折叠起来！

2.3 逐板分析

• 这是一个非常机械的模式，棋盘从左到右整齐排列。
• 每一步的贡献都从很小开始，逐渐变大，在中间达到最大，然后又开始缩小。
• 我们的进展有点难以预测。当然，在中途，我们已经完成了半圈，但模式时高时低，难以分析。相比之下，每一圈的图案每次变化的量都是一样的，总是在增加。很明显，后面几环的工作量最大。在这里，似乎是中间部分在做最繁重的工作。

首先是甲板和木结构。在铺设木板时，我们不希望走回头路（尤其是涉及到其他步骤时，比如油漆）。就像一棵树的每一步都需要一个完整的圆一样，露台也坚持使用我们能在家得宝（Home Depot）找到的线性木板。

事实上，任何有严格 “流水线 ”的流程都可能使用这种方法：完成一个部分，然后进入下一个部分。想一想打印机，它必须在纸张通过时喷出图案（或者现在的 3d 打印机）。打印机只能看到一个位置一次，所以最好让它计数！

圆圈不一定是字面上的形状。它可以代表你要实现的目标，无论是锻炼计划还是心理咨询中要涉及的主题。

棋盘式方法建议你从小处着手，逐步提高，然后再慢慢降低。披萨片式方法可以忍受（每天都有相同的进步），但环形方法可能会打击士气：每走一步都需要付出比前一步更多的努力。

2.4 有条不紊

到目前为止，我们一直在使用自然描述来解释我们的想法： “取一堆圆环 “或 ”把圆切成披萨片"。这虽然传达了一个笼统的概念，但有点像用 “嘟-嘟-嘟 ”来描述一首歌--可能只有你自己知道你在说什么。不过，稍加整理就能让你的意图一目了然。

首先，我们可以解释一下如何将形状分成几个步骤。我喜欢想象一个小箭头，指示我们在切割每一块时的移动方向：

在我的脑海中，我沿着黄线移动，一边走一边喊着步骤（向前一步，做一个环，向前一步，做一个环......）。

虽然箭头显示了圆环的制作过程，但由于步骤被卡在圆圈里，所以很难想象出来。正如我们在第一课中看到的，我们可以把各个步骤拉出来，然后把它们排成一排：

我们画一个黑色箭头来显示每个台阶大小的变化趋势。很不错吧？我们一眼就能看出，环数在增加，而且每次增加的数量都一样（趋势线是直的，就像楼梯一样）。

数学迷和神经质的人都喜欢把棋子排成一排。我想，这有一种抚慰人心的作用：谁不想把散落在地上的铅笔排成一行呢？

既然说到这个话题，我们不妨也整理一下其他图案：

啊！现在比较每种 X-Ray 策略就容易多了：

• 使用圆形环时，步数稳步增加（上斜线）
• 使用三角形切片时，台阶大小保持不变（平直的水平线）
• 使用矩形板时，台阶变大，达到顶峰，然后变小（向上和向下）。趋势线看起来被拉长，是因为木板被推到了底部。
• 这些图表让策略比较变得更容易了，你说呢？当然，但等等，这条趋势线看起来不就像可怕的 X-Y 图吗？

没错。不幸的是，许多课程只是简单地展示黑色趋势线，而不向你展示它所代表的棋子。这就是痛苦的秘诀：明确图形的含义！

黑色趋势线是对 X-Ray 策略的超级概括描述。我们显示的是每一块的大小（图表高度）以及它们的大小是如何变化的（趋势方向）。

环形、片状和板状之间的区别并不重要：在微积分中，它们都是整个模式的组成部分。片“、”环 “或 ”板 “等词只是 ”整体的一部分"的描述性版本，在其他方面可以互换。

在本指南中，我们将把图表保持在上述水平：趋势线，并显示各个部分。这是为以后基于性能的课程打下基础，在这些课程中，你可以直接使用图形。但仅供参考，阿基米德在没有 x-y 图形的情况下奠定了微积分的基础，并在没有图形的情况下发现了他的结果。

参考资料

• 软件测试精品书籍文档下载持续更新 https://github.com/china-testing/python-testing-examples 请点赞，谢谢！
• 本文涉及的python测试开发库 谢谢点赞！ https://github.com/china-testing/python_cn_resouce
• python精品书籍下载 https://github.com/china-testing/python_cn_resouce/blob/main/python_good_books.md
• Linux精品书籍下载 https://www.cnblogs.com/testing-/p/17438558.html

3 将X光战略带入三维空间？

3d与2d类似：

• 有机过程是逐层贝壳生长的（牡蛎中的珍珠）。
• 公平分割需要楔形（为朋友切苹果）。
• 机器人平板方法似乎很容易制造（举重平板）。
• 橘子是一种有趣的混合体：从外表看，它似乎是由贝壳制成的，随着时间的推移不断生长。但在内部，它形成了一个对称的楔形内部结构--有利于种子的均匀分布，对吗？我们可以从两个方面来分析它。

3.1 探索三维视角

在第一课中，我们模糊地认为圆/球公式是相关的：

有了 X-Ray 和 Time-Lapse 技能，我们就有了具体的概念：

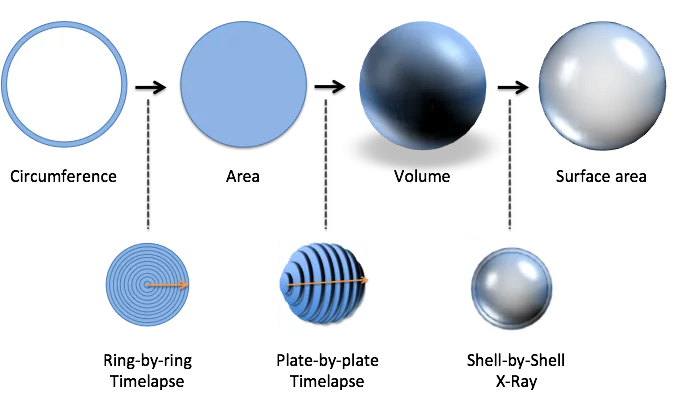
• 圆周率： 从单个圆环开始。
• 面积： 用逐环延时法制作填充圆盘。
• 体积： 将圆环做成一个盘子，然后逐个盘子延时制作一个球体。
• 表面积： 用 X 射线将球体照成一堆外壳；外壳就是表面积。

哇 我们现在可以详细描述一个公式与另一个公式的关系了。凭直觉，我们知道如何通过思考 “延时摄影这个 ”或 “X 射线那个 ”将形状变形为其他版本。我们甚至可以逆向思维：从一个球体开始，用 X 射线把它变成板块，然后再用 X 射线把一个板块变成环形。

3.2 数学符号的必要性

你可能已经注意到，描述你的想法越来越难了。我们需要用物理类比（圆环、木板、楔子）来解释我们的计划： “好吧，把这个圆形区域做成一些圆盘。对，就像这样。现在把这些圆盘排成球形......"。

我喜欢图表和类比，但是否应该要求用它们来解释一个想法呢？也许不需要。

看看数字是如何发展起来的。起初，我们使用非常直观的符号来计数： I、II、III，等等。最后，我们意识到像 V 这样的符号可以代替 IIIII，而且更好的是，每个数字都可以有自己的符号。(数字 “1 ”让我们想起了以线条为基础的历史）。

数学符号在几个方面发挥了作用：

• 符号比文字短。
• 规则为我们工作。使用罗马数字时，我们基本上是在手工创建数字（为什么写 VIII 要比写 I 花那么多力气？就因为 8 比 1 大？这不是个好理由！）。小数帮助我们 “完成 ”表达数字的工作，并使它们易于操作。到目前为止，我们一直在自己做微积分的工作：把一个圆切成环形，意识到我们可以把它们展开，查找面积方程并测量得到的三角形。难道规则在这里帮不了我们吗？当然可以。我们只需要弄清楚它们。
• 归纳了我们的思维。“2+3=5 “其实就是 ”2+3=5"。这听起来很奇怪，但我们有了一个抽象的量（不是人、钱或牛......只是 “twoness”），我们就知道了它与其他量的关系。算术规则是通用的，而我们的工作就是把它们应用到具体场景中。

最后一点很重要。在学习加法时，老师可能会用苹果的字面意义来表示 2 加 3 等于 5。经过足够的练习，你开始使用抽象的符号，而不需要物理例子，“2 + 3 = 5 ”就变得有意义了。

微积分与此类似：它适用于抽象方程，如：

在应用微积分技巧时，我们可以真正看到微积分的作用，而不是推来推去的符号。最终，我们可以将图形转换为相应的等式，并直接使用符号进行运算。

因此，不要认为微积分需要一个现实世界的物体，就像加法需要苹果一样。它可以分析任何形状或公式（物理方程、商业场景、函数图）--只是形状更容易入门。