交通规划四阶段法:基于 Python 的交通分布预测算法复现 - 附完整代码链接
交通规划四阶段法:基于 Python 的交通分布预测算法复现 - 附完整代码链接
我这个学期有交通规划的课程。·交通规划四阶段法中第二阶段即是交通分布预测,需要使用一些常用的算法,常见的像是:
- 传统的增长系数方法:平均系数法、底特律法、Frater法、Funess法等
- 重力模型:无约束重力模型、单约束重力模型法、双约束重力模型法
我写了一些算法简单的 Python 实现,封装成了 Python 类和函数,以便调用。当然,实际的交通需求预测当中不会真的使用 Python 之类的代码工具来实现,有现成的专用工具,如 TransCAD 等。此处代码仅做一演示,以便 课堂测试计算的时候偷懒 学习交流使用。
到目前为止算法的完成度并不高,只有简单的几个模型。对于已经完成的代码部分,大家可以自行取用。但是 比起分享现在已经完成的代码,我更希望有人可以和我一起合作写代码。因此我将项目发布挂在了 Gitee 平台,理想的话希望可以发展成一个 Python 包。
项目的页面地址:基于 Python 的交通分布预测算法复现
拉取项目的命令:
git clone https://gitee.com/BOXonline_1396529/traffic_distribution_predict.git
我只是想使用这些代码
如果您只是想使用这些代码来学习算法或者完成您的课堂作业,以下是你需要做的事:
下载代码文件
看这篇博客的小伙伴们应该有很多都是和我一样的苦逼交通生,可能从来没有在开放代码平台下载过代码,找不到下载按钮。其实下载按钮就在网页的这个位置:
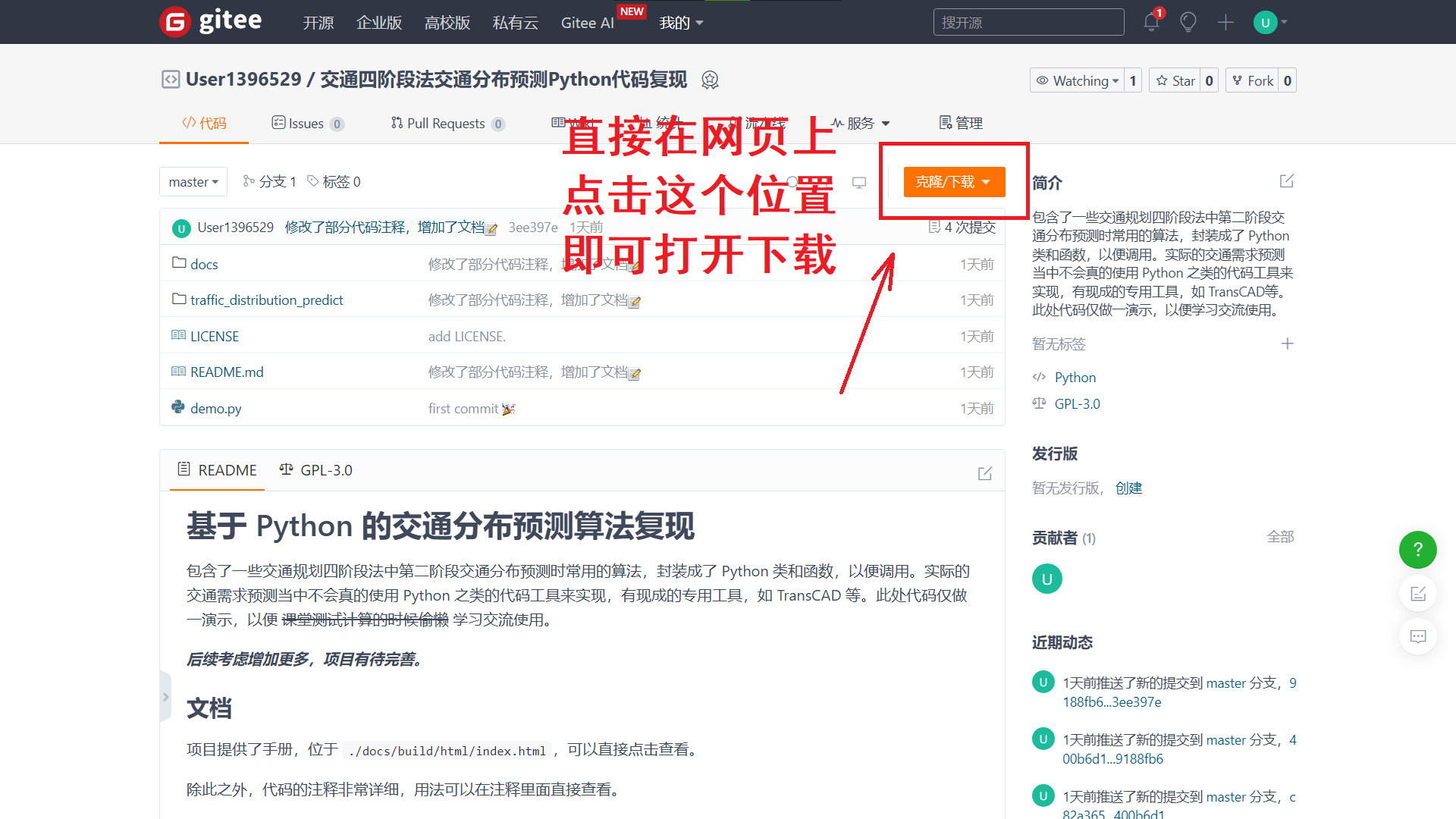
最近的 Gitee 有点烦人,可能会让你扫码关注公众号注册之类的。稍微应付一下就好了哈。
点击之后会弹出这个窗口:

直接下载 .zip 就是代码的压缩包了。
代码的使用方法
为防止交通专业的同学们不会用这些代码,特此说明:你可以像使用一般的模块那样使用这些代码。确保项目根目录下的 traffic_distribution_predict 目录与您需要调用模块的代码文件(.py、.ipynb 等)处于同一目录下。导入需要的工具,这里以福莱特法交通分布预测函数为例:
from traffic_distribution_predict.coefficient_model import frator
然后调用函数:
# 需要计算的数据
# `X` 为 OD 矩阵
# `U` 和 `V` 分别为未来年的生成量与吸引量
X = np.array([[17,7,4],[7,38,6],[4,5,17]])
U = np.array([38.6, 91.9, 36.0])
V = np.array([39.3, 90.3, 36.9])
# `fX` 为未来年 OD 矩阵
fX = frator(X, U, V, alpha=0.05)
具体的用法可以参考项目根目录下的 .\docs\build\html\index.html 文件,双击在浏览器中打开。也可以参考详细的代码注释。
合作
如果您想要参与项目合作,您可以:
- 与我取得联系
- 提交 Issues
- 克隆仓库到本地,编写代码,提交 Pull Requests
部分代码内容的展示
以下是部分代码内容的展示,选取了 无约束重力模型 作为演示。
"""
traffic_distribution_predict.gravity_model
==========================================
实现基于 **重力模型** 的交通分布预测。
在交通分布预测中,重力模型(Gravity model)是一种广泛应用
的模型,其灵感来源于物理学中的万有重力定律。在交通领域,这个
模型用于预测从一个地区到另一个地区的流量(如人口流动、交通流
量等)。
模型假设两地区之间的流量与两地区的吸重力成正比,与两地区之间
的距离的某个函数成反比。
"""
import numpy as np
import statsmodels.api as sm
class unconstrained_gravity_model:
r"""
使用无约束重力模型进行交通分布预测
这个类实现了使用 **无约束重力模型** 进行交通分布预测的功能
无约束重力模型的基本形式(无约束重力模型)可以表示为:
.. math::
q_{ij} = k \frac{O_i^{\alpha} O_j^{\beta}
}{C_{ij}^{\gamma}}
无约束重力模型包含 :math:`\alpha`、:math:`\beta`、
:math:`\gamma`,参数通过参数估计方法取得。具体的参数估计
方法是对模型两侧得取对数,从而转化为线性回归模型的形式:
.. math::
\ln(q_{ij}) = {
\ln(\alpha) + \beta \ln(Oi \cdot Dj) - {
\gamma \ln(c_{ij})}}
令上式中各个参数项:
- :math:`y = \ln(q_{ij})`
- :math:`a_0 = \ln(\alpha)`
- :math:`a_1 = \beta`
- :math:`a_2 = -\gamma`
则可对应如下的线性回归模型:
.. math::
Y = a_0 + a_1 x_1 + a_2 x_2
通过对线性模型进行求解和参数的转换,可以实现无约束重力模型的
参数估计。其中,线性模型的求解依赖 `statsmodels.api.OLS`
,您有必要安装 `statsmodels`。
使用下面的命令安装 `statsmodels`:
.. code-block:: shell
pip install statsmodels
输入参数
----------
X : numpy.array
交通原始的 OD 矩阵,要求行列数相等
C : numpy.array
交通现状下各个交通小区之间往返所需的行驶时间,是交通
距离的量化,要求行列数相等
类的方法
----------
__init__(X, C) :
类的初始化方法
fit() :
拟合模型
OLS_summary() :
输出一元线性回归模型的详细信息
predict(U, V, fC):
预测未来年的交通 OD 矩阵,将直接输出 OD 矩阵
示例
----------
假设已经存在 3*3 的 OD 矩阵 `X` 和 代表各个交通小区之间往返
所需的行驶时间的矩阵 `C`,可以创建模型:
>>> X = np.array([[17,7,4],[7,38,6],[4,5,17]])
>>> C = np.array([[7,17,22],[17,15,23],[22,23,7]])
>>> gravity_model = unconstrained_gravity_model(X, C)
使用 `.fit()` 方法可以拟合模型,直接返回的元组即模型的三
参数:math:`\alpha`、:math:`\beta`、:math:`\gamma`,
逐一对应。
>>> gravity_model.fit()
(0.12445664474836608,
1.1726892457872755,
1.4553127410580864)
如果需要模型根据当前年的交通现状预测未来年的交通分布,则需要
未来年各个交通小区的交通发生量 `U`、吸引量 `V`,以及未来年
各个交通小区之间往返所需的行驶时间的矩阵 `fC`
>>> fC = np.array([[4,9,11],[9,8,12],[11,12,4]])
>>> U = np.array([38.6, 91.9, 36.0])
>>> V = np.array([39.3, 90.3, 36.9])
调用 `.predict()` 进行预测
>>> gravity_model.predict(U, V, fC)
array([[ 88.94742489, 72.49109653, 18.95286558],
[ 75.57580647, 237.96479061, 46.18126501],
[ 18.80408686, 43.94860253, 76.12489132]])
其他参照
----------
:class:`statsmodels.api.OLS`
`statsmodels` 提供的线性回归工具
"""
def __init__(self, X, C):
"""
类的初始化方法
输入参数
----------
X : numpy.array, m=n
交通原始的 OD 矩阵
C : numpy.array, m=n
交通现状下各个交通小区之间往返所需的行驶时间
"""
# 将函数参数给到类属性
self.OD_mat = X
self.distance_mat = C
# 取得交通小区的个数,交通小区个数即 OD 矩阵长度
self.n = len(self.OD_mat)
# 计算总吸引量和总生成量
self.O = np.sum(self.OD_mat, axis=1) # 横向求和
self.D = np.sum(self.OD_mat, axis=0) # 纵向求和
def fit(self):
"""
拟合模型
返回值
-------
tuple
包含重力模型三参数的元组,形如:
`(self.alpha, self.beta, self.gamma)`
示例
-------
>>> gravity_model.fit()
(0.12445664474836608,
1.1726892457872755,
1.4553127410580864)
"""
# `x_1` 和 `x_2` 两个列表就能储存取对数后的数值
# 这样的变量命名方式是为了和数学公式里的表述对应以便理解
x_1 = [] # 对 $O_i$ 和 $D_j$ 取对数的结果
x_2 = [] # 对距离矩阵 `distance_mat` 每一项取对数
y = [] # 对原始 OD 矩阵取对数
# 通过循环填充列表
for i in range(self.n):
for j in range(self.n):
y.append(np.log(self.OD_mat[i][j]))
x_1.append(np.log(self.O[i]*self.D[j]))
x_2.append(
np.log(self.distance_mat[i][j])
)
# 组织训练线性回归模型的数据
train_X = np.array([x_1, x_2]).T
train_y = y
# `statsmodels.api.OLS` 默认没有截距项
# 这里需要手动加入截距
train_X_with_bias = sm.add_constant(train_X)
self.results = sm.OLS( # 注意参数排列的顺序
train_y, train_X_with_bias
).fit() # 直接拟合模型
# 获取线性回归模型参数
self.OLS_params = self.results.params
# 根据公式计算模型参数
self.alpha = np.e ** (self.OLS_params[0])
self.beta = self.OLS_params[1]
self.gamma = -self.OLS_params[2]
self.params = (self.alpha, self.beta, self.gamma)
return self.params
def predict(self, U, V, fC):
"""
利用拟合好的模型,根据当前年的交通现状预测未来年的交通分布
输入参数
----------
U : numpy.array
未来年各交通小区的总生成量,行向量
V : numpy.array
未来年各交通小区的总吸引量,行向量
fC : numpy.array
各个交通小区之间往返所需的行驶时间
返回值
-------
numpy.array
预测的未来年各交通小区交通量
示例
-------
如果需要模型根据当前年的交通现状预测未来年的交通分布,则需要
未来年各个交通小区的交通发生量 `U`、吸引量 `V`,以及未来年
各个交通小区之间往返所需的行驶时间的矩阵 `fC`
>>> fC = np.array([[4,9,11],[9,8,12],[11,12,4]])
>>> U = np.array([38.6, 91.9, 36.0])
>>> V = np.array([39.3, 90.3, 36.9])
调用 `.predict()` 进行预测
>>> gravity_model.predict(U, V, fC)
array([[ 88.94742489, 72.49109653, 18.95286558],
[ 75.57580647, 237.96479061, 46.18126501],
[ 18.80408686, 43.94860253, 76.12489132]])
"""
self.future_O = U
self.future_D = V
self.future_distance_mat = fC
self.q = np.zeros(self.OD_mat.shape)
# 根据公式计算 q_ij
for i in range(self.n):
for j in range(self.n):
self.q[i][j] = (
self.alpha * (
((self.future_O[i] * self.future_D[j]) ** self.beta
) / (
self.future_distance_mat[i][j] ** self.gamma
)))
return self.q