A星搜索算法的更多细节
A*搜索算法的更多内容
A*算法,也许你会习惯称它为「A*寻路算法」。许多人大概是因寻路——尤其是「网格地图」寻路认识它的,网上很多教程也是以网格地图为例讲解它的算法实现。这导致了许多人在遇到同样用了A*算法的地方,例如GOAP或者基于八叉树的立体空间寻路时会一头雾水:A*算法原来有这么多「变种」吗(⊙ˍ⊙)?其实A*算法是没有变的,只是我们原先 错误地将它与「网络地图」捆绑在了一起。A*算法本身是一种 搜索算法,这次我们从另一视角看看「A*搜索算法」,并一起完成一个更泛用的「A*搜索器」,最后再探讨一些常见的正确优化方式与错误优化方式。
注意:本文并不会详细将A*算法的逻辑原理,希望你至少已了解用于网格地图的A*寻路算法 ̄へ ̄,本文算是对《人工智能:一种现代的方法(第3版)》第三章以及《游戏人工智能(Game AI Pro)2015版》第17讲相关内容的「复述」,感兴趣的同学可以亲自看看呀~
1. 启发式的搜索策略
「宁滥勿缺」的 「 广度优先搜索(Breath First Search,简称BFS)」和「不撞南墙不回头」的「 深度优先搜索(Depth First Search,简称DFS)」是最为人所知的两种 「盲目搜索策略」 。相比于它们的「一根筋」,有些搜索策略通过 记录些额外信息 就能更清楚地知道往哪搜索 「更有希望」 接近目标,这类搜索策略就是 「启发式搜索策略」 。
我们要讲的A*搜索算法就是启发式搜索策略中最出名的一种,你一定还记得A*算法中的这个式子:f(n) = g(n) + h(n)
这里的g(n)表示 从开始节点 到当前的n节点已经花费的代价,而h(n)表示 该节点 到目标节点 所需的估计代价。可以看出,f(n)可谓「瞻前顾后」,其中h(n),即启发式函数(heuristic function)的设计便是关键所在。
2. 陌生的启发式函数
如果你学过用于网格地图寻路的A*搜索算法的同学,一定会想到h(n)的几种设计方式,比如曼哈顿距离、欧式距离、对角线估价……但这些都是针对网格地图,如果我们面对的是中继点图(Waypoint)呢?

你一时或许的确不知道该怎么设计h(n),但这没关系,你应该清楚的是A*搜索算法的逻辑依旧没变,让我们对A*感到陌生的原因仅仅是 启发式函数不同 而已。
h(n)会根据搜索问题的不同而不同,比如,在GOAP中h(n)需要被设计为能估计当前状态与目标状态的接近程度的函数,这比起寻路时的距离估计明显抽象了不少。但设计h(n)依旧是有思路可循的:
- 可采纳性。可采纳性是指h(n)从不会过高(超过实际的)估计到达目标的代价。也就是说要「乐观」,h(n)估计的到达目标的代价值要小于实际执行时的代价。比如,我们在网格地图寻路时,一般都不会采用曼哈顿距离。因为我们都知道:三角形的两边之和大于第三边,假设实际中,当前节点n与目标节点就是一条线过去,那么曼哈顿距离这种「横平竖直」的估计方式就导致 估计值 > 实际值,不够「乐观」。

- 一致性。对于用于图搜索的A*算法,通常h(n)都是满足一致性的。「一致」说的是这么一回事:假设,现在处于n节点,我们可以采取任一行动抵达下个节点n1(下图中由红圈表示),我们需要保证 h(n) 不能大于「n→n1花费的代价 + h(n1) 」,通俗地说就是「不能与过去的h(n)的预测相矛盾」,如果h(n)不满足一致性的话,即 h(n) > 「n→n1花费的代价 + h(n1) 」,很明显h(n)的就不满足可采纳性了。这样的h(n)无法保障找到最优解。

3. 泛用的A*搜索算法
了解了这些,我们可以开始设计A*算法的通用结构了。首先要考虑搜索的节点:
- 大多数情况下,我们需要记录节点的 父节点 以便搜索完成时可以回溯生成路径;
- 节点 自身也有代价 ,用于表示从其他节点走向这个节点时的花费代价(就像之前提到的「n→n1花费的代价」);
- 节点都应当有用于 记录f(n)、g(n)、h(n)的值;
- 节点都有 邻居节点 。如果一个节点没有邻居节点就意味着它不可抵达,就没必要纳入搜索;
- 由于启发式函数的设计需要,节点需要 衡量从当前节点到目标节点代价的函数。
考虑到这些,我们可以将A*的节点以接口方式实现:
using System.Collections.Generic;
public interface IAStarNode<T> where T : IAStarNode<T>
{
public T Parent { get; set; }//父节点,通过泛型使它的类型与具体类一致
public float SelfCost { get; set; }//自身单步花费代价
public float GCost { get; set; }//记录g(n),距初始状态的代价
public float HCost { get; set; }//记录h(n),距目标状态的代价
public float FCost { get; }//记录f(n),总评估代价
/// <summary>
/// 获取与指定节点的预测代价
/// </summary>
public float GetDistance(T otherNode);
/// <summary>
/// 获取后继(邻居)节点
/// </summary>
/// <param name="nodeMap">寻路所在的地图,类型看具体情况转换,
/// 故用object类型</param>
/// <returns>后继节点列表</returns>
public List<T> GetSuccessors(object nodeMap);
}
这样一来,我们只需要让充当节点的具体类继承这个接口,实现这其中的两个函数,就能参与A*搜索了。当然,在有些情况下可能一个节点还要额外记录它所连接的边(比如GOAP),这些就是需要在具体类中额外添加的内容了。
终于,到了 「A*搜索器」 的设计,经过前面已经反复强调了:A*搜索算法本身的逻辑是不变的,变化的只是启发式函数。而我们已经把启发式函数的设计留在节点类的GetDistance了,所以我们可以设计出一个通用的搜索器。
A*搜索器只负责搜索(寻路)并返回搜索的序列结果(路径),而这个任务可以分为:
- 维护openList与closeList。 这是A*搜索所依赖的额外信息,在搜索过程中,那些有被搜过但还没被选中要走的节点就会放在「边缘集(openList)」中 ;而已经走过的节点则会放在「搜索集(closeList)」中。A*搜索便会不断地将结点加入到openList以备选,并不断地将走过的节点加入closeList以避免重复搜索。
- 生成路径。 在找到了目标(或实在找不到目标)时,我们需要返回一路走来的所有结点,我们要考虑这些点的顺序,而且最好能将路径返回到一个外部容器中存储,而不是函数内创建用于存储的容器再返回出去。为什么?因为大多数情况下,我们是为对象单独分配一个搜索的结果,比如每个角色都有自己的路径,这是个一对一的关系。如果采用后者的方案,那么即便只有一个角色要寻路,我们也会每次在生成路径时,就会重复创建容器并返回,是十分浪费的。
下面就来看看具体代码吧:
using System.Collections.Generic;
/// <summary>
/// A星搜索器
/// </summary>
/// <typeparam name="T_Map">搜索的图类</typeparam>
/// <typeparam name="T_Node">搜索的节点类</typeparam>
public class AStar_Searcher<T_Map, T_Node> where T_Node: IAStarNode<T_Node>, IMyHeapItem<T_Node>
{
private readonly HashSet<T_Node> closeList;//探索集
private readonly MyHeap<T_Node> openList;//边缘集
private readonly T_Map nodeMap;//搜索空间(地图)
public AStar_Searcher(T_Map map, int maxNodeSize = 200)
{
nodeMap = map;
closeList = new HashSet<T_Node>();
//maxNodeSize用于限制路径节点的上限,避免陷入无止境搜索的情况
openList = new MyHeap<T_Node>(maxNodeSize);
}
/// <summary>
/// 搜索(寻路)
/// </summary>
/// <param name="start">起点</param>
/// <param name="target">终点</param>
/// <param name="pathRes">返回生成的路径</param>
public void FindPath(T_Node start, T_Node target, Stack<T_Node> pathRes)
{
T_Node currentNode;
pathRes.Clear();//清空路径以备存储新的路径
closeList.Clear();
openList.Clear();
openList.PushHeap(start);
while (!openList.IsEmpty)
{
currentNode = openList.Top;//取出边缘集中最小代价的节点
openList.PopHeap();
closeList.Add(currentNode);//拟定移动到该节点,将其放入探索集
if (currentNode.Equals(target) || openList.IsFull)//如果找到了或图都搜完了也没找到时
{
GenerateFinalPath(start, target, pathRes);//生成路径并保存到pathRes中
return;
}
UpdateList(currentNode, target);//更新边缘集和探索集
}
return;
}
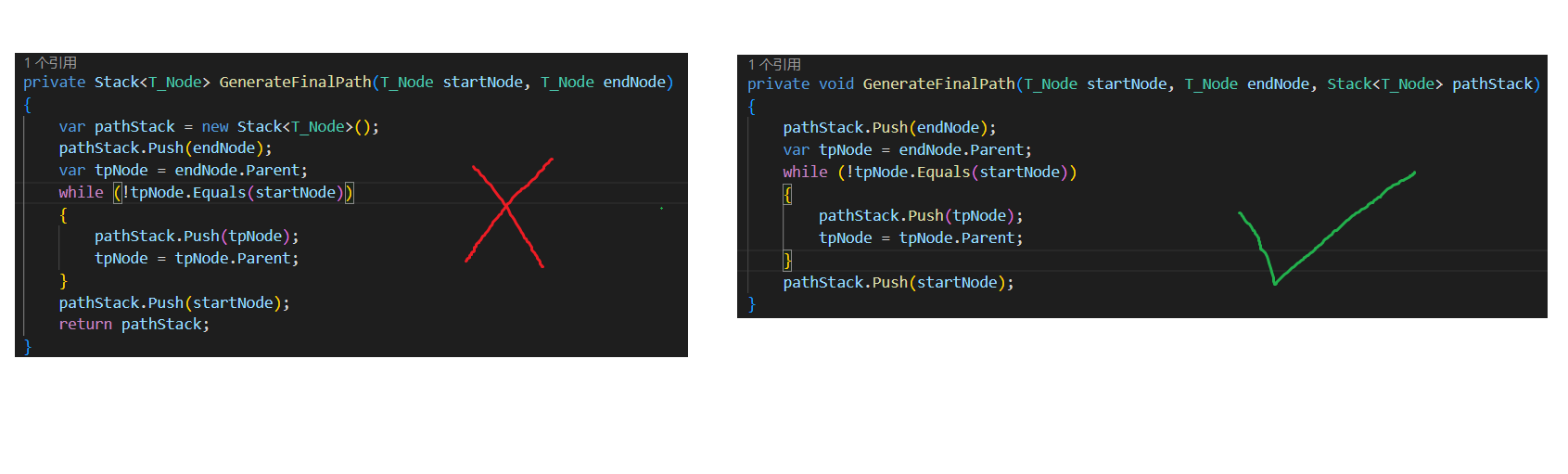
private void GenerateFinalPath(T_Node startNode, T_Node endNode, Stack<T_Node> pathStack)
{
pathStack.Push(endNode);//因为回溯,所以用栈储存生成的路径
var tpNode = endNode.Parent;
while (!tpNode.Equals(startNode))
{
pathStack.Push(tpNode);
tpNode = tpNode.Parent;
}
pathStack.Push(startNode);
}
private void UpdateList(T_Node curNode, T_Node endNode)
{
T_Node sucNode;
float tpCost;
bool isNotInOpenList;
var successors = curNode.GetSuccessors(nodeMap);//找出当前节点的后继节点
for (int i = 0; i < successors.Count; ++i)
{
sucNode = successors[i];
if (closeList.Contains(sucNode))//后继节点已被探索过就忽略
continue;
tpCost = curNode.GCost + sucNode.SelfCost;
isNotInOpenList = !openList.Contains(sucNode);
if (isNotInOpenList || tpCost < sucNode.GCost)
{
sucNode.GCost = tpCost;
sucNode.HCost = sucNode.GetDistance(endNode);//计算启发函数估计值
sucNode.Parent = curNode;//记录父节点,方便回溯
if (isNotInOpenList)
{
openList.PushHeap(sucNode);
}
}
}
}
}
上面有用到自己实现的优先队列(MyHeap),如果你也有自己的实现也可以进行替换。如果没有的话,可以暂时用用我的:
using System;
public interface IMyHeapItem<T> : IComparable<T>
{
public int HeapIndex { get; set; }
}
public class MyHeap<T> where T : IMyHeapItem<T>
{
public int NowLength { get; private set; }
public int MaxLength { get; private set; }
public T Top => heap[0];
public bool IsEmpty => NowLength == 0;
public bool IsFull => NowLength >= MaxLength - 1;
private readonly bool isReverse;
private readonly T[] heap;
public MyHeap(int maxLength, bool isReverse = false)
{
NowLength = 0;
MaxLength = maxLength;
heap = new T[MaxLength + 1];
this.isReverse = isReverse;
}
public T this[int index]
{
get => heap[index];
}
public void PushHeap(T value)
{
if (NowLength < MaxLength)
{
value.HeapIndex = NowLength;
heap[NowLength] = value;
Swim(NowLength);
++NowLength;
}
}
public void PopHeap()
{
if (NowLength > 0)
{
heap[0] = heap[--NowLength];
heap[0].HeapIndex = 0;
Sink(0);
}
}
public bool Contains(T value)
{
return Equals(heap[value.HeapIndex], value);
}
public T Find(T value)
{
if (Contains(value))
return heap[value.HeapIndex];
return default;
}
public void Clear()
{
for (int i = 0; i < NowLength; ++i)
{
heap[i].HeapIndex = 0;
}
NowLength = 0;
}
private void SwapValue(T a, T b)
{
heap[a.HeapIndex] = b;
heap[b.HeapIndex] = a;
(b.HeapIndex, a.HeapIndex) = (a.HeapIndex, b.HeapIndex);
}
private void Swim(int index)
{
int father;
while (index > 0)
{
father = (index - 1) >> 1;
if (IsBetter(heap[index], heap[father]))
{
SwapValue(heap[father], heap[index]);
index = father;
}
else return;
}
}
private void Sink(int index)
{
int largest, left = (index << 1) + 1;
while (left < NowLength)
{
largest = left + 1 < NowLength && IsBetter(heap[left + 1], heap[left]) ? left + 1 : left;
if (IsBetter(heap[index], heap[largest]))
largest = index;
if (largest == index) return;
SwapValue(heap[largest], heap[index]);
index = largest;
left = (index << 1) + 1;
}
}
private bool IsBetter(T v1, T v2)
{
return isReverse ? (v2.CompareTo(v1) < 0 ): (v1.CompareTo(v2) < 0);
}
}
4. 正确优化A*的方式
- 良好的启发式函数。 前面我们讨论的那些正好可以说明这一点,故不再赘述。
- 合适的搜索空间表示。 「搜索空间」可以理解为我们要来寻路的地图,合适的表示能够减少搜索时的结点数量,从而减少搜索时间。一般的表示方式有:网格图、中继点图、导航网络。
(虽说一般也只能自主设计前面两种就是了

- 预分配所有必要的内存。 就是说,在实际搜索时不要分配内存,当然,这并不是说不能使用临时变量,只是说不要使用需要分配大量内存的临时变量,比如一个大数组。如果真有需要,也可以使用像「内存池」提前分配好内存,避免重复的开辟与回收。
- 用优先队列做开结点表(openList)。 A*搜索时常需要找出「开结点表」中最小代价的结点。如果使用「优先队列(一般二叉堆即可)」就可以省去排序的过程,以O(1)的时间复杂度找到这个结点。
- 缓存后继节点。 在静态场景中,一个节点的后继节点(邻居节点)通常是固定的,如果我们在查找一次后就将它们记录下来,那么后续查找可以节省很多时间(因为查找节点的邻居是很经常的事),只不过需要额外的内存开销。
5. 错误优化A*的方式
-
并行执行多个搜索。 通过多线程,我们可以在只消耗一次搜索的时间里同时处理10个搜索,这不是很好吗?问题在于,如果你要同时进行10次搜索,那势必要在单独多开一些openList和closeList,这 需要大量的内存 。而且如果在这10次搜索中,有一次搜索情况「不顺」导致它 拖延了其它的搜索 ,又当如何(做好搜索上限判断,这种情况一般就不会发生)?其实也不是不能使用多线程,我们可以同时只执行2个搜索,一个负责处理较为快速的搜索,另一个负责处理需要长时间的搜索。
-
双向搜索。 可能有些同学曾做过一些搜索相关(主要是关于BFS和DFS)的算法题,发现「双向搜索」似乎能更快地找到路径。但其实这对于A*搜索,会 花费双倍的工作量 。我们可以看看下面几张图(横着看):


通过这两次寻路不难看出,正向寻路所得的路径和反向寻路的 路径重合度非常低 ,换句话说,几乎就是找了两条路。如果你不信,也可以自己动手试试看,在这个网页中找到下图部分,自己编辑下地形、切换起点和终点,观察路径情况。

造成这现象的一大原因,就是正反搜索时同一个节点的h(n)是不同的。因此,如下图般理想的双向搜索,在A*中是很难见到的。

-
缓存路径。 有时可能会想:将这次找到的路保存下来,下次再找时可以直接调用。这种做法的价值并不大,「两次相同的寻路」概率并不大,而且保存过多的路径会占用很大的内存。
6. 尾声
在我初学A*时,总以为它是基于网格寻路而生的一种算法,希望这次与大家交流的内容也能帮助曾经和我一样有类似想法的同学更准确地认识A*。
热门相关:黑暗血时代 1号婚令:早安,大总裁! 我和超级大佬隐婚了 盛华 三国之袁氏枭雄