一套模板搞定二叉树算法题--二叉树算法讲解002
1、二叉树的递归
递归:

2、二叉树遍历之DFS深度优先遍历
2.1、遍历的概念

每个节点 都要恰好被访问一次,本质上是二叉树的线性化 。
一个树形的结构,线性化为一个数组之类的"串"的结构。
2.2、DFS深度优先遍历

示例二叉树原型图:
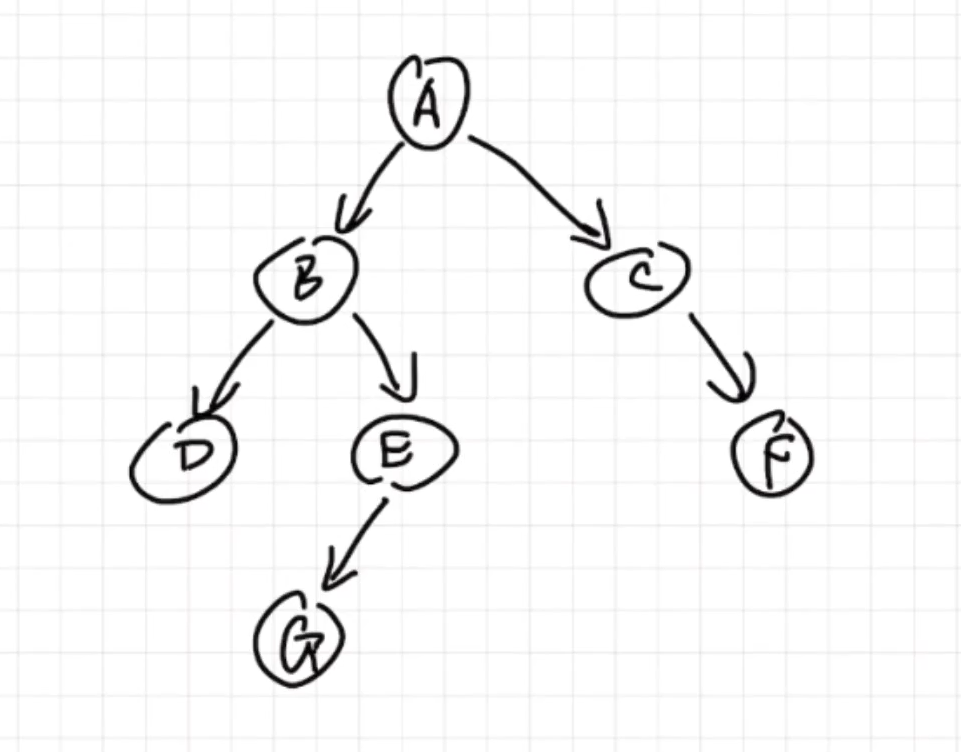
2.2.1、前序遍历
前序遍历执行顺序:
根节点--对左子树做前序遍历--对右子树做前序遍历
总的顺序:根节点--左子树--右子树
左子树中:根-左-右
根节点
右子树中:根-左-右

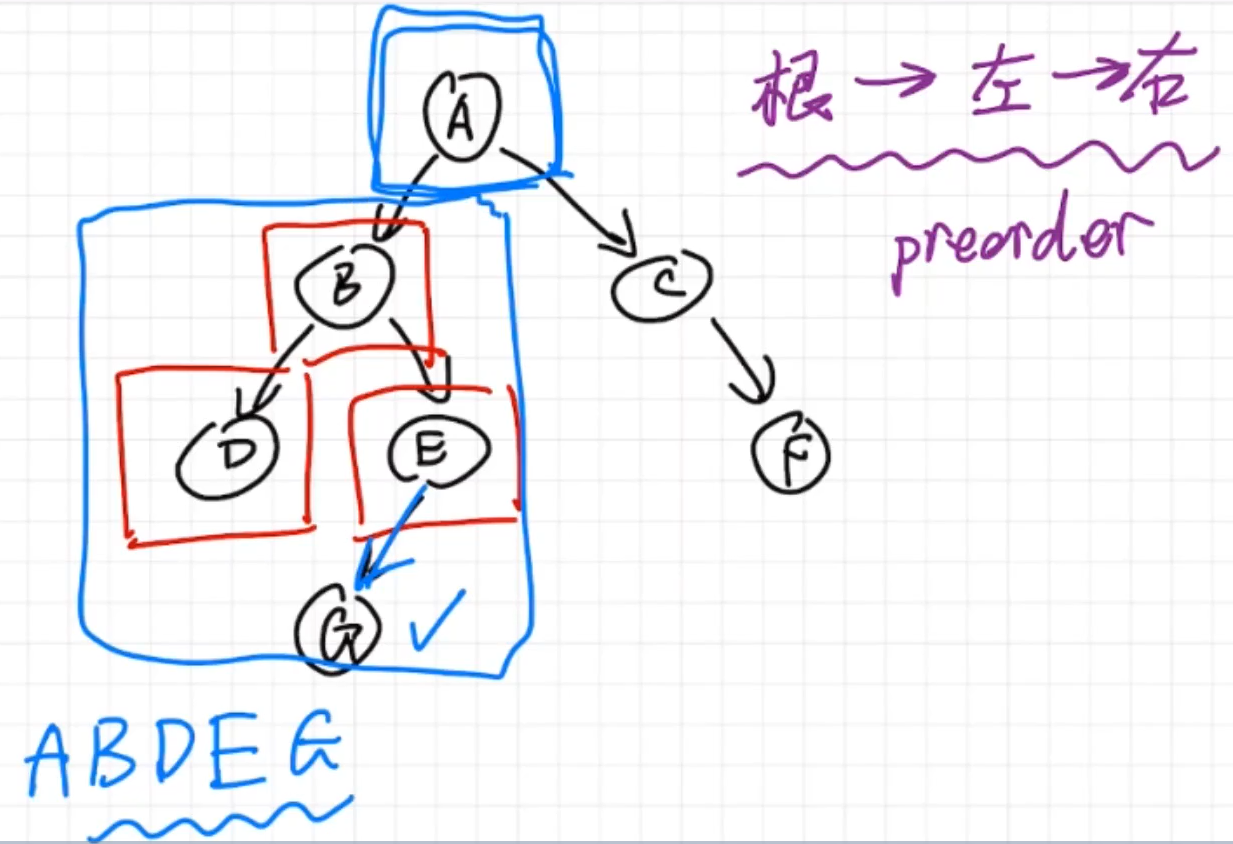
对A的左子树做前序遍历

A的左子树的根节点是B

对B的左子树做前序遍历

对B的右子树做前序遍历


对E的左子树前序遍历

至此,A的左子树做完了前序遍历:
然后,对A的右子树做前序遍历:

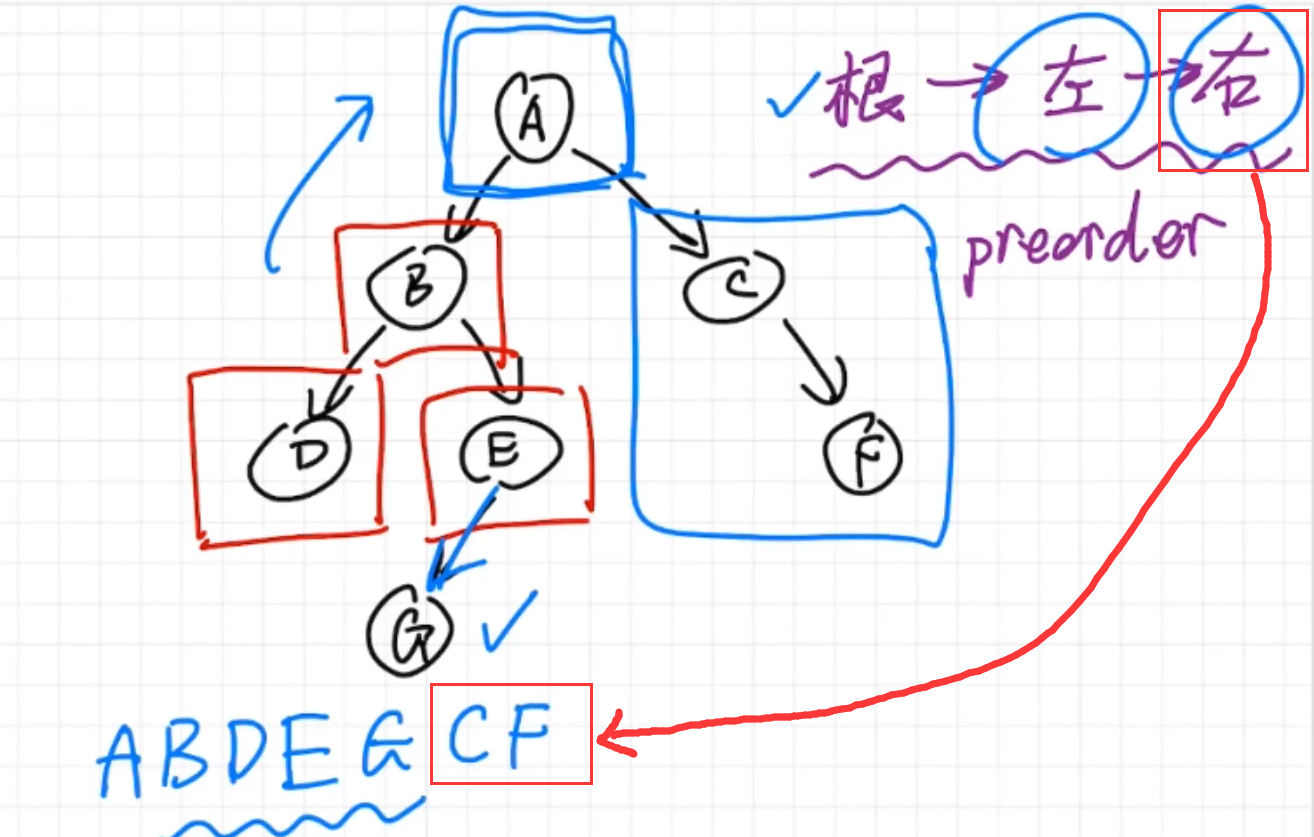
至此,二叉树的前序遍历完成。
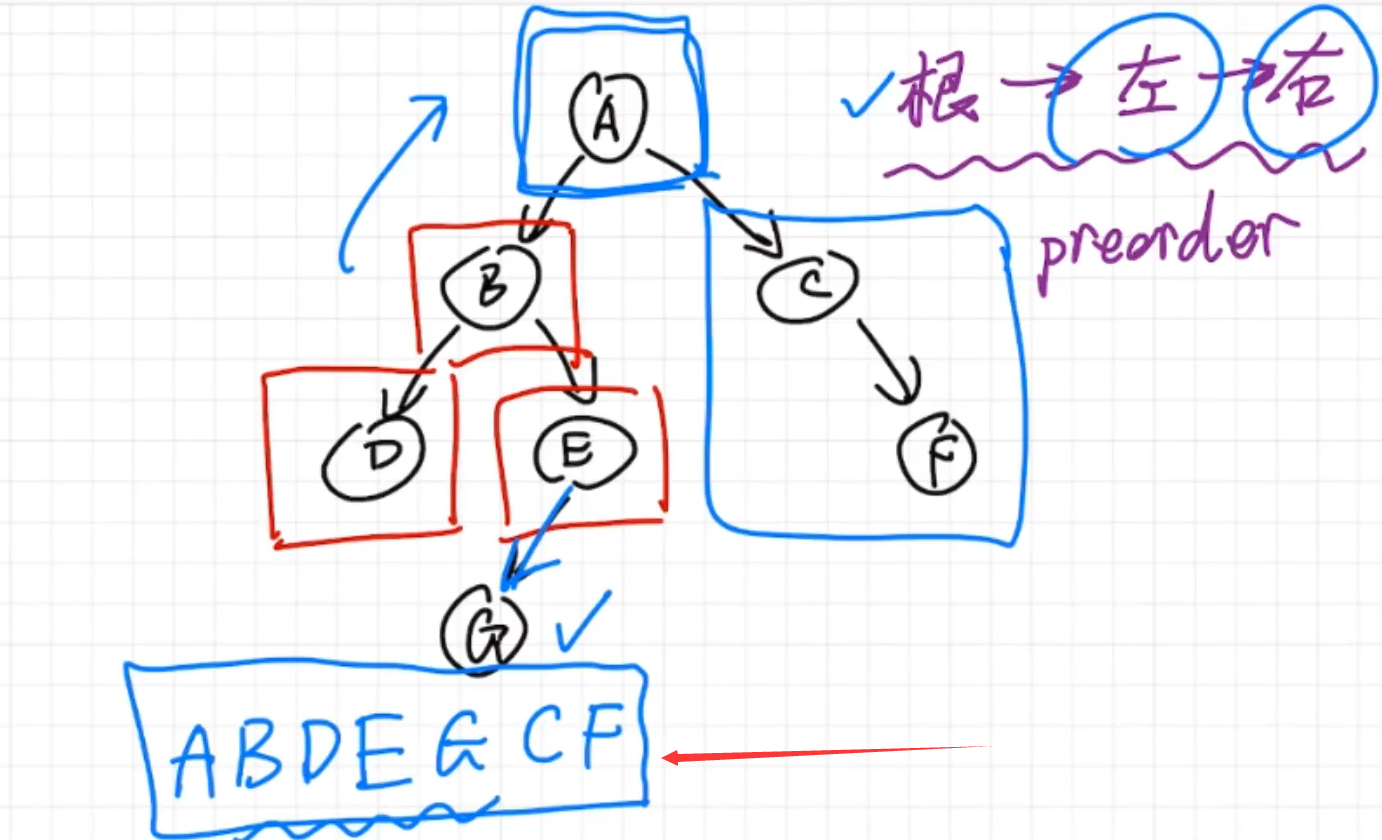
我们会发现,整个深度优先的遍历过程都是 递归的。
2.2.2、中序遍历
中序遍历执行顺序:
对左子树做中序遍历--根节点--对右子树做中序遍历
总的顺序:左子树--根节点--右子树
左子树中:左--根-右
根节点
右子树中:左-根-右
2.2.3、后序遍历
后序遍历执行顺序:
对左子树做后续遍历--对右子树做后续遍历--根节点
总的顺序:左子树--右子树--根节点
左子树中:左--右-根
根节点
右子树中:左-右-根
2.2.4、总结
所谓前序、中序、后序的区别。
就是根在前、根在中、还是根在后?
左、右的顺序都是不变的,从左到右。

3、DFS深度优先遍历之代码实现

4、二叉树三种深度遍历
4.1 leetcode 144 前序遍历


4.2 leetcode 94 中序遍历

4.3 leetcode 145 后序遍历
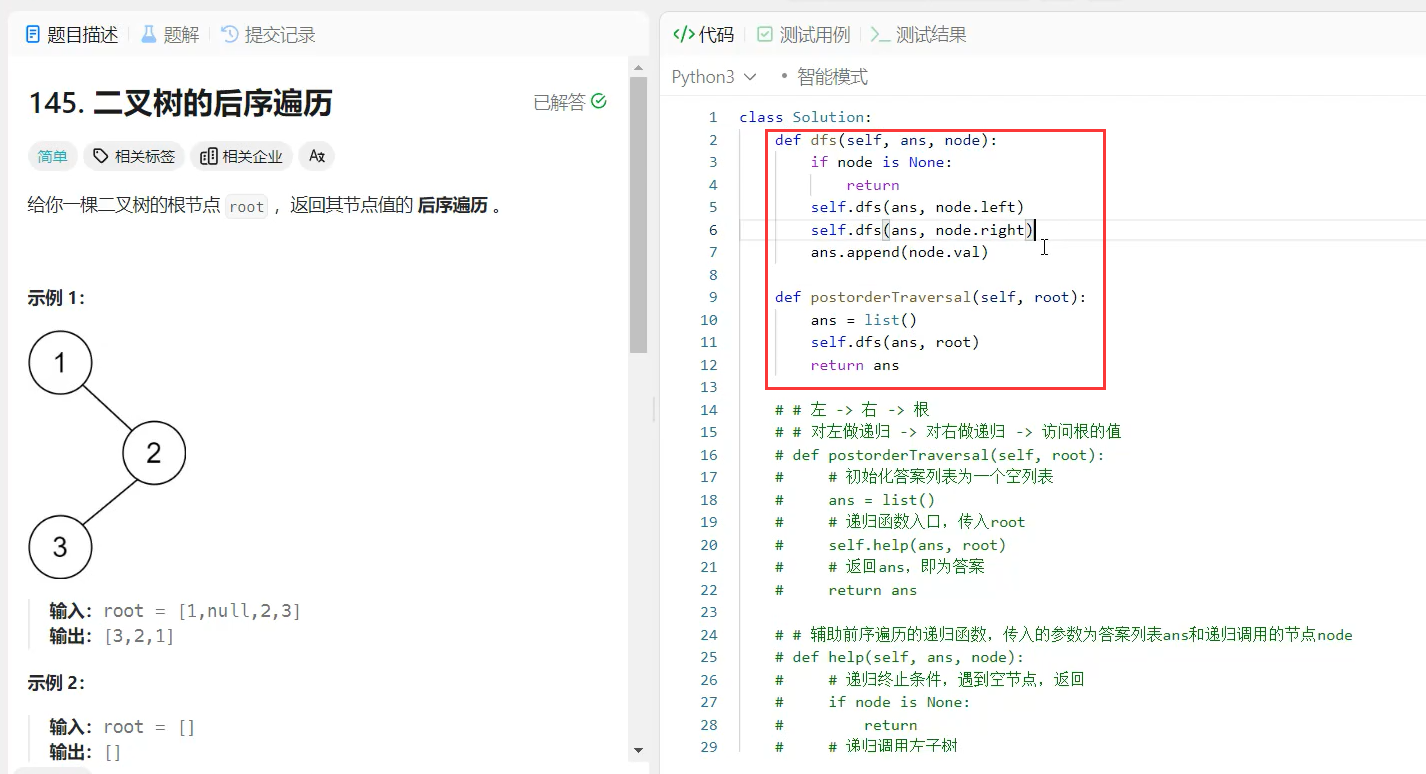
5、从深度遍历序列还原二叉树--经典题
5.1、leetcode105 从前序与中序遍历序列构造二叉树
题目:
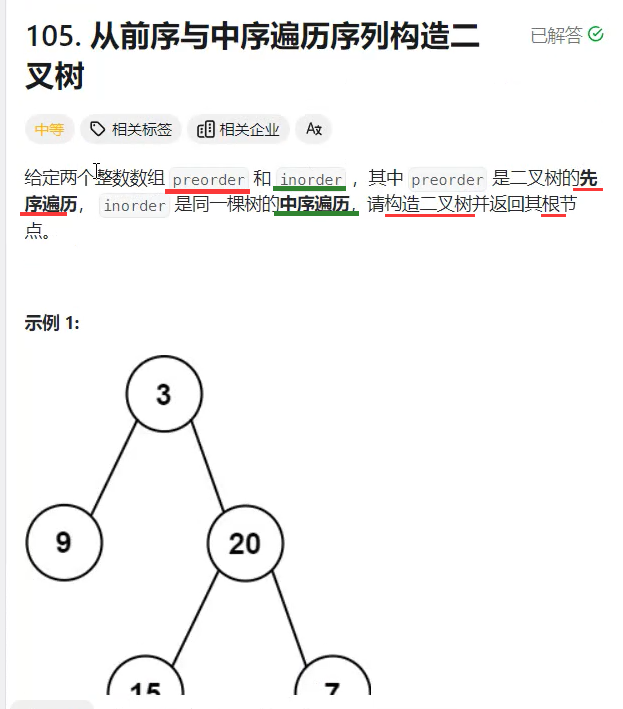
题意:

题解思路:

前序:
前序的根:

前序的根确定为3

再根据中序确定左右子树



根据前序和中序的遍历规则确定20为右子树的根:

总结步骤:
1、根据提供的前序数组的第一个元素,确定二叉树的根节点
2、找到根节点后,在中序数组中,根据根节点切割左右
左边为二叉树左子树内容,右边为二叉树右子树内容
3、再将中序数组切割的左右,返回给前序,在重复步骤1、2做递归操作
再来一个示例树讲解步骤,强调递归的体现:

找到根节点3和左子树、右子树


递归右子树:

右子树的根节点20和左子树、右子树


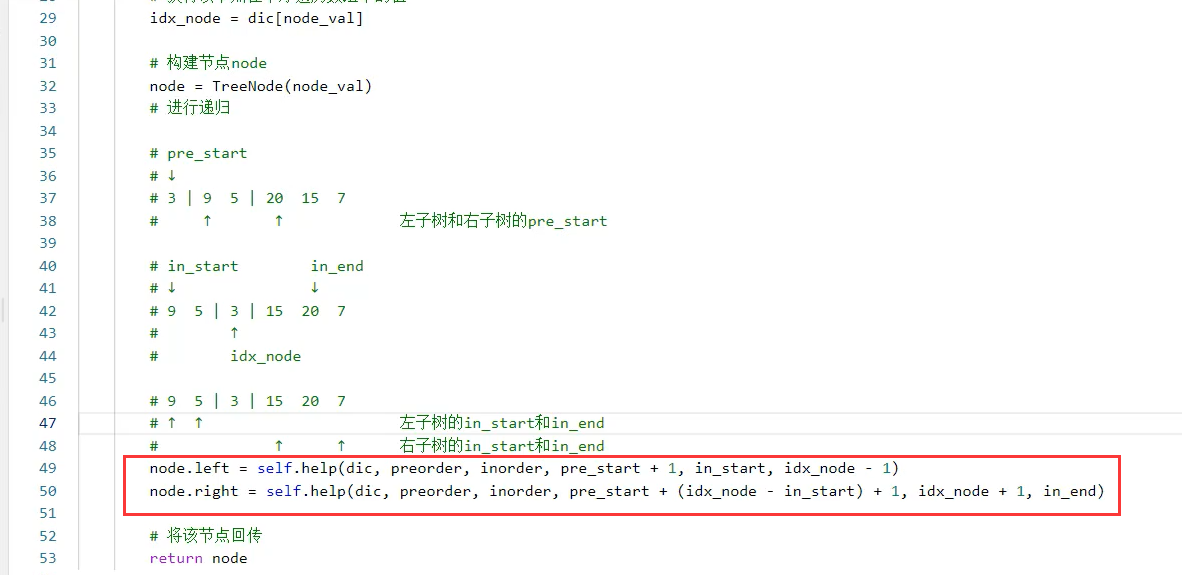
核心思路:
其实是个子数组的过程,即把2个大数组(前序和中序数组)不断拆成更小的数组的过程
1个大数组的拆分过程,可以使用2个指针来做拆分这件事
实现过程中重要的3个指针:
pre_start、in_start、in_end、同时也会用到代表根节点的idx
3个指针的含义:

图解:


递归:
下一次递归左子树时:
pre_start 是 pre_start+1
in_start还是in_start不变
in_end是idx-1
下一次递归右子树时:
pre_start 是 pre_start + (idx - in_start)+ 1
in_start是idx+1
in_end还是in_end
这样我们就可以实现递归了。
可以再看一个类似的示例图:

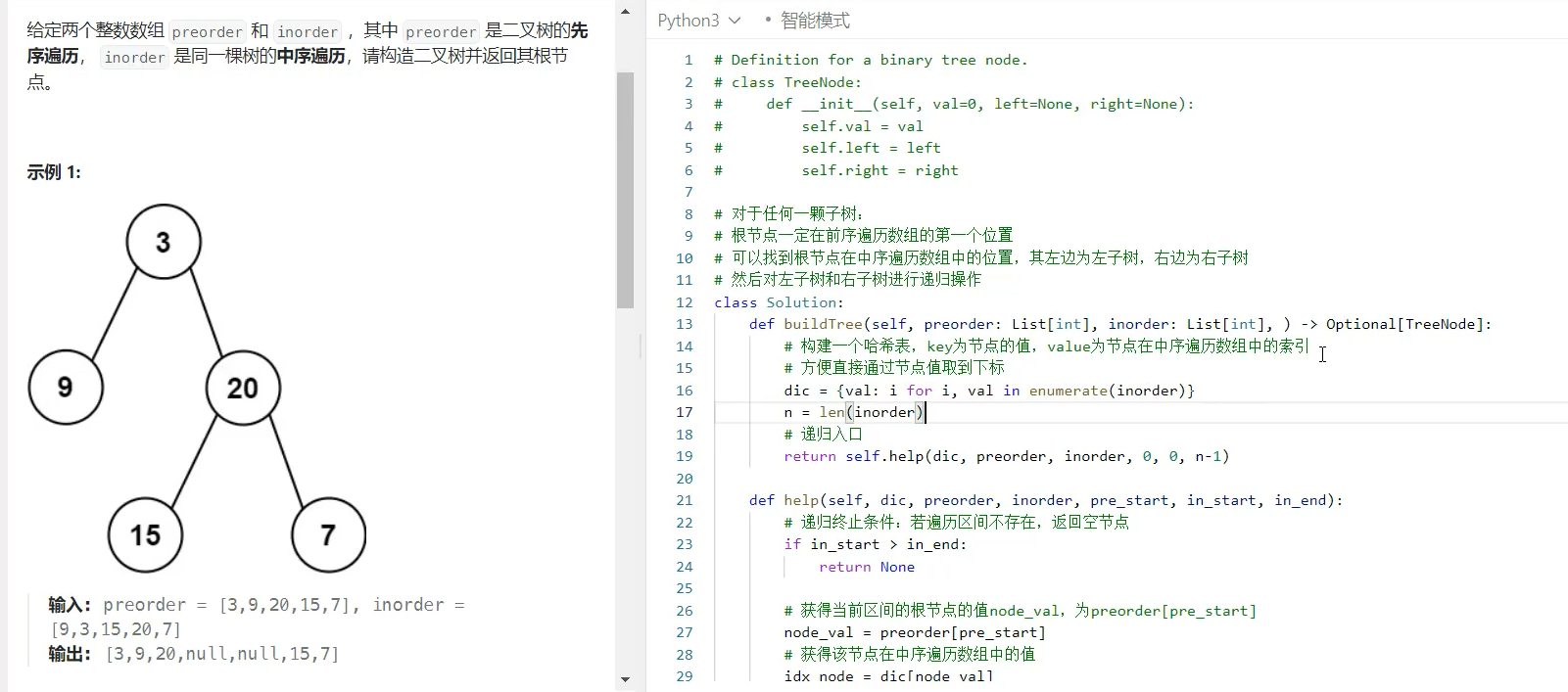
题解:

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
# 对于任何一颗子树:
# 根节点一定在前序遍历数组的第一个位置
# 可以找到根节点在中序遍历数组中的位置,其左边为左子树,右边为右子树
# 然后对左子树和右子树进行递归操作
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int], ) -> Optional[TreeNode]:
# 构建一个哈希表,key为节点的值,value为节点在中序遍历数组中的索引
# 方便直接通过节点值取到下标
dic = {val: i for i, val in enumerate(inorder)}
n = len(inorder)
# 递归入口
return self.help(dic, preorder, inorder, 0, 0, n-1)
def help(self, dic, preorder, inorder, pre_start, in_start, in_end):
# 递归终止条件:若遍历区间不存在,返回空节点
if in_start > in_en
return None
# 获得当前区间的根节点的值node_val,为preorder[pre_start]
node_val = preorder[pre_start]
# 获得该节点在中序遍历数组中的位置
idx_node = dic[node_val]
# 构建节点node
node = TreeNode(node_val)
# 进行递归
# pre_start
# ↓
# 3 | 9 5 | 20 15 7
# ↑ ↑ 左子树和右子树的pre_start
# in_start in_end
# ↓ ↓
# 9 5 | 3 | 15 20 7
# ↑
# idx_node
# 9 5 | 3 | 15 20 7
# ↑ ↑ 左子树的in_start和in_end
# ↑ ↑ 右子树的in_start和in_end
node.left = self.help(dic, preorder, inorder, pre_start + 1, in_start, idx_node - 1)
node.right = self.help(dic, preorder, inorder, pre_start + (idx_node - in_start) + 1, idx_node + 1, in_end)
# 将该节点回传
return node
注:
代码中的 {val: i for i, val in enumerate(inorder)} 表示我们将 inorder 列表中的每个元素作为字典的键,将其索引作为对应的值。
例如,如果 inorder 是 [4, 2, 7, 5, 1, 3, 6] ,那么生成的字典 dic 将是 {4: 0, 2: 1, 7: 2, 5: 3, 1: 4, 3: 5, 6: 6} 。
5.2、leetcode106 从中序与后序遍历序列构造二叉树
题目:


题解:

5.3、2023C-二叉树的广度优先遍历
题目:

题意和思路:
先根据中序和后序遍历构造二叉树,再进行二叉树的层序遍历
相当于leetcode106和leetcode102这2题的组合。

6、二叉搜索树
6.1、二叉搜索树的概念和性质

6.2、二叉搜索树的查找

查找n次,每次有2个分支中的1个;
即为: \(2^n = k\)
\(n = log_2^k\)
每次查找只进入2个分支中的1个,所以时间复杂度为O(log(n))
可以理解为一种特殊的二分查找,和二分查找的时间复杂度是一样的。
或者说二叉搜索树是二分查找在树形结构上的体现。
6.2.1、二叉搜索树查找代码模板

6.2.2、二叉搜索树查找--leetcode 700
题目和题意:

题解:
注意思考,递归子问题为什么要return?

如果对上述的return的写法不熟悉,可以改为如下使用成员变量的写法:
初始化成员变量 self.ans = None


6.3、二叉搜索树的增加

6.3.1、二叉搜索树的增加 -- leetcode 701
题目和题意:
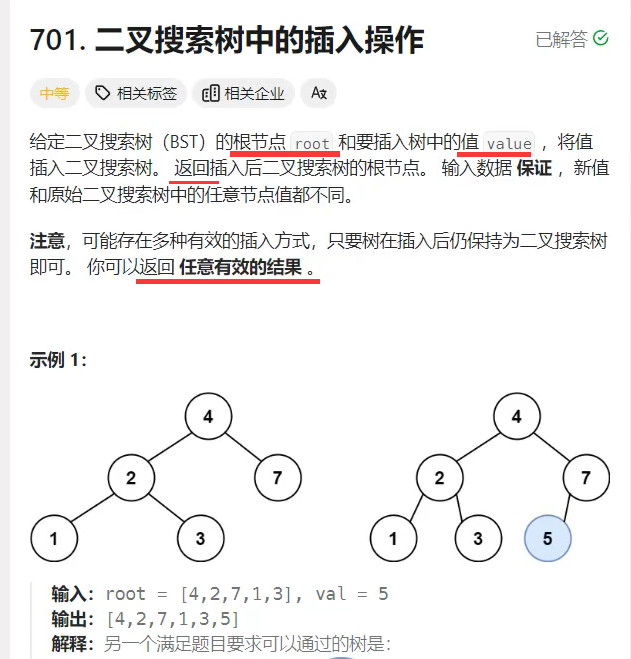
题解:

6.3.2、二叉搜索树的增加 -- 2023C 计算三叉搜索树的高度
题目和题意

题解:
这题其中关键部分的解法(树的插入部分)和 leetcode 701几乎一样。

6.3.3、二叉搜索树的增加 -- leetcode 98 验证二叉搜索树
题目:
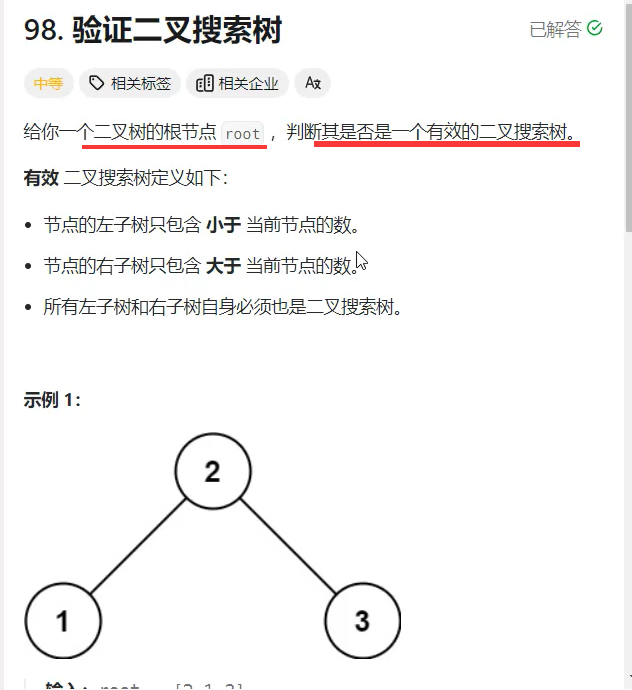

解题思路:
用二叉搜索树的性质
①、先中序遍历出树
②、再判断树的值是否从小到大排列的。

其中步骤1就是leetcode94 中序遍历二叉树。
题解:

注:
步骤1中序遍历二叉树可以这样实现
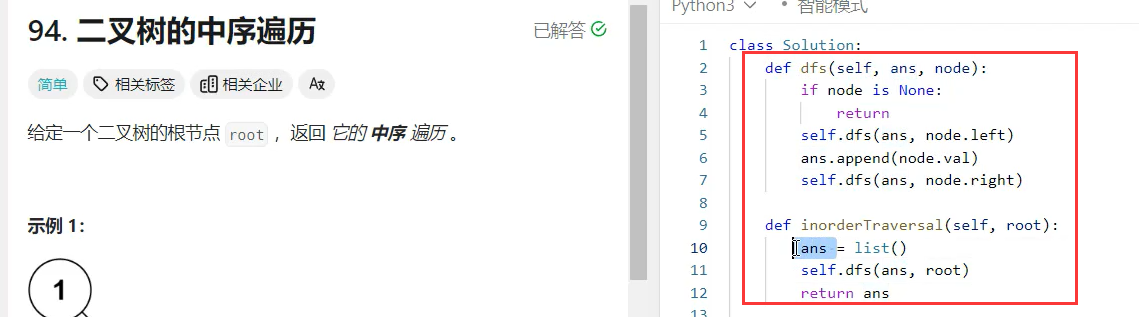
也可以这样回传列表的方式实现 实现的方式多种多样

7、总结

注:
文中截图源自大佬: 闭着眼睛学数理化 课程内容