UNCTF-Crypto wp

2023-12-01 14:15 由 Kicky_Mu 发表于 #其他

2020年

easy_rsa

题目

from Crypto.Util import number
import gmpy2
from Crypto.Util.number import bytes_to_long

p = number.getPrime(1024)
q = number.getPrime(1024)
if p > q:
    a = p + q
    b = p - q
    print(a,b)

n = p * q
e = 65537
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = bytes_to_long(b'msg')
c = pow(m,e,n)
print(c)

#320398687477638913975700270017132483556404036982302018853617987417039612400517057680951629863477438570118640104253432645524830693378758322853028869260935243017328300431595830632269573784699659244044435107219440036761727692796855905230231825712343296737928172132556195116760954509270255049816362648350162111168
#9554090001619033187321857749048244231377711861081522054479773151962371959336936136696051589639469653074758469644089407114039221055688732553830385923962675507737607608026140516898146670548916033772462331195442816239006651495200436855982426532874304542570230333184081122225359441162386921519665128773491795370
#22886015855857570934458119207589468036427819233100165358753348672429768179802313173980683835839060302192974676103009829680448391991795003347995943925826913190907148491842575401236879172753322166199945839038316446615621136778270903537132526524507377773094660056144412196579940619996180527179824934152320202452981537526759225006396924528945160807152512753988038894126566572241510883486584129614281936540861801302684550521904620303946721322791533756703992307396221043157633995229923356308284045440648542300161500649145193884889980827640680145641832152753769606803521928095124230843021310132841509181297101645567863161780

我的解答：

已知

a = p + q

b = p - q

故：a + b = 2p 由此可得出p 同理相减可得q

exp：

import gmpy2
from Crypto.Util.number import *

a = 320398687477638913975700270017132483556404036982302018853617987417039612400517057680951629863477438570118640104253432645524830693378758322853028869260935243017328300431595830632269573784699659244044435107219440036761727692796855905230231825712343296737928172132556195116760954509270255049816362648350162111168
b = 9554090001619033187321857749048244231377711861081522054479773151962371959336936136696051589639469653074758469644089407114039221055688732553830385923962675507737607608026140516898146670548916033772462331195442816239006651495200436855982426532874304542570230333184081122225359441162386921519665128773491795370
c = 22886015855857570934458119207589468036427819233100165358753348672429768179802313173980683835839060302192974676103009829680448391991795003347995943925826913190907148491842575401236879172753322166199945839038316446615621136778270903537132526524507377773094660056144412196579940619996180527179824934152320202452981537526759225006396924528945160807152512753988038894126566572241510883486584129614281936540861801302684550521904620303946721322791533756703992307396221043157633995229923356308284045440648542300161500649145193884889980827640680145641832152753769606803521928095124230843021310132841509181297101645567863161780
e = 65537
p = (a+b)//2
q = (a-b)//2
n = p * q
phi = (p-1) * (q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(long_to_bytes(m))
#UNCTF{welcome_to_rsa}

鞍山大法官开庭之缺的营养这一块怎么补

题目：

某日，鞍山大法官在点外卖时点了2个韭菜盒子，商家只送了1个，大法官给了该商家一个差评
次日，该大法官又在该商家点了1个韭菜盒子，希望商家能补上上次的韭菜盒子，而商家又只发了一个韭菜盒子
这名大法官一天正常要吃2个韭菜盒子，而该商家每天只给他1个韭菜盒子，请问该名大法官缺的营养这一块怎么补
ottttootoootooooottoootooottotootttootooottotttooootttototoottooootoooottotoottottooooooooottotootto
flag格式：unctf{}

我的解答：

考点：培根密码

分别把o和t替换为A和B，培根解密

ABBBBAABAAABAAAAABBAAABAAABBABAABBBAABAAABBABBBAAAABBBABABAABBAAAABAAAABBABAABBABBAAAAAAAAABBABAABBA

unctf{PEIGENHENYOUYINGYANG}

简单的RSA

题目

你们都不会百度的吗

e= 18437613570247445737704630776150775735509244525633303532921813122997549954741828855898842356900537746647414676272022397989161180996467240795661928117273837666615415153571959258847829528131519423486261757569454011940318849589730152031528323576997801788206457548531802663834418381061551227544937412734776581781
n= 147282573611984580384965727976839351356009465616053475428039851794553880833177877211323318130843267847303264730088424552657129314295117614222630326581943132950689147833674506592824134135054877394753008169629583742916853056999371985307138775298080986801742942833212727949277517691311315098722536282119888605701
c= 140896698267670480175739817539898638657099087197096836734243016824204113452987617610944986742919793506024892638851339015015706164412994514598564989374037762836439262224649359411190187875207060663509777017529293145434535056275850555331099130633232844054767057175076598741233988533181035871238444008366306956934

我的解答：

考点：维纳攻击

exp:

import gmpy2
from Crypto.Util.number import *

def transform(x, y):  # 使用辗转相处将分数 x/y 转为连分数的形式
    res = []
    while y:
        res.append(x // y)
        x, y = y, x % y
    return res


def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return denominator, numerator  # 得到渐进分数的分母和分子，并返回


# 求解每个渐进分数
def sub_fraction(x, y):
    res = transform(x, y)
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def get_pq(a, b, c):  # 由p+q和pq的值通过维达定理来求解p和q
    par = gmpy2.isqrt(b * b - 4 * a * c)  # 由上述可得，开根号一定是整数，因为有解
    x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
    return x1, x2


def wienerAttack(e, n):
    for (d, k) in sub_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)
        px, qy = get_pq(1, n - phi + 1, n)
        if px * qy == n:
            p, q = abs(int(px)), abs(int(qy))  # 可能会得到两个负数，负负得正未尝不会出现
            d = gmpy2.invert(e, (p - 1) * (q - 1))  # 求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元d
            return d
    print("该方法不适用")

e= 18437613570247445737704630776150775735509244525633303532921813122997549954741828855898842356900537746647414676272022397989161180996467240795661928117273837666615415153571959258847829528131519423486261757569454011940318849589730152031528323576997801788206457548531802663834418381061551227544937412734776581781
n= 147282573611984580384965727976839351356009465616053475428039851794553880833177877211323318130843267847303264730088424552657129314295117614222630326581943132950689147833674506592824134135054877394753008169629583742916853056999371985307138775298080986801742942833212727949277517691311315098722536282119888605701
c= 140896698267670480175739817539898638657099087197096836734243016824204113452987617610944986742919793506024892638851339015015706164412994514598564989374037762836439262224649359411190187875207060663509777017529293145434535056275850555331099130633232844054767057175076598741233988533181035871238444008366306956934 
d = wienerAttack(e, n)
print("d=", d)
m = pow(c, d, n)
print(long_to_bytes(m))
#unctf{wi3n3r_Att@ck}

wing

你过office二级了吗

我的解答：

题目提示office，猜测为word中某种字体，打开word输入字母+数字，再切换各字体核对，发现为Wingdings 2字体，对照替换得flag。

unctf{wingdings_is_incomprehensible}

Really baby problem about block cipher
flag 格式： flag{}

题目

查看代码

 import random
from Crypto.Cipher import AES
from os import urandom
from string import printable
from binascii import hexlify
from secret import flag

random.seed(urandom(32))

key1 = '0'*13 + ''.join([random.choice(printable) for _ in range(3)])
key2 = ''.join([random.choice(printable) for _ in range(3)]) + '0'*13

cipher1 = AES.new(key=key1.encode(), mode=AES.MODE_ECB)
cipher2 = AES.new(key=key2.encode(), mode=AES.MODE_ECB)

pt = input("You have a chance to get something: ")
pt = pt.encode()

val = len(pt) % 16
if not val == 0:
    pt += b'\x00'*(16 - val)

c1 = cipher1.encrypt(pt)
c2 = cipher2.encrypt(c1)
print('Your cipher:{}'.format(hexlify(c2)))

assert(len(flag) % 16 == 0)
c3 = cipher1.encrypt(flag)
c4 = cipher2.encrypt(c3)
print('Your flag:{}'.format(hexlify(c4)))

You have a chance to get something: UNCTF2020_Enjoy_Crypto~
Your cipher:b'01a4e429e76db218fa0eb18f03ec69c9200a2362d8b4d7ea46170ce698389bbd'
Your flag:b'196cc94c2d685beb54beeaa14c1dc0a6f3794d65fca0d1a1274515166e4255ab367383092e42d774992f74bc138faaad'

我的解答：

AES-ECB模式两次加密，且密钥已知位较多，爆破一下即可

exp:


from string import printable
import itertools
from Crypto.Cipher import AES
from binascii import hexlify, unhexlify

pt = b'UNCTF2020_Enjoy_Crypto~'
val = len(pt) % 16
if not val == 0:
    pt += b'\x00'*(16 - val)
    print("pt==",pt)
yan= unhexlify(b'01a4e429e76db218fa0eb18f03ec69c9200a2362d8b4d7ea46170ce698389bbd')
print(yan)

table = {}

for p1 in itertools.product(printable, repeat=3):
    key = "".join(p1)
    key1 = "0000000000000"+key
    cipher1 = AES.new(key=key1.encode(), mode=AES.MODE_ECB)
    c1 = cipher1.encrypt(pt)
    table[c1] = key1

for p2 in itertools.product(printable, repeat=3):
    key = "".join(p2)
    key2 = key+"0000000000000"
    cipher2 = AES.new(key=key2.encode(), mode=AES.MODE_ECB)
    c2 = cipher2.decrypt(yan)
    # print("c2==",c2)
    if c2 in table:
        key1 = table[c2]
        print(key1, key2)
        break

flag = b"196cc94c2d685beb54beeaa14c1dc0a6f3794d65fca0d1a1274515166e4255ab367383092e42d774992f74bc138faaad"
flag = unhexlify(flag)
for key in [key2, key1]:
    cipher = AES.new(key=key.encode(), mode=AES.MODE_ECB)
    flag = cipher.decrypt(flag)
    print(flag)
#unctf{524e314a-5843-3030-5939-333230323541}

快乐数学_0x00

刚才我问扎克利，扎总发生甚么事了。扎总说怎么回事。我给扎总发了几张截图。
扎总一看，噢，原来是昨天，几个大学生，二十多岁，他们说，哎~。
有一个说，我在 UNCTF 打比赛，头都做疼了，扎总，你能不能教教我怎么做题，哎，帮我分数弄高一点。
扎总说，可以，你在 UNCTF 死做题，不好用。他不服气。
扎总说，我说小朋友，你多长两个脑子来做我这新题。他做不动，他说你这个没用。
扎总说，我这个有用，他是数学，数学对计算机基础很重要，二百多个人做不出我这题。他非要和我试试。
扎总说，可以。扎总一说他啪站起来了，很快啊，然后上来一个左正蹬，一个右鞭腿，一个左刺拳。
扎总全部防出去了啊，防出去以后，自然是传统功夫以点到为止，右手把数学题摁在他鼻子上，没打他，扎总笑了一下，准备收拳。
后面我暂时编不下去了，你们来跟扎总打吧。
数学题，可能存在异议的，群里私聊 Hanser 的老公。

链接: https://pan.baidu.com/s/1nB8j4TN3HFe_SXvrwzyE2g 密码: ca04

我的解答：

纯高数计算，我们可采用wolframalpha辅助计算。

首先对与：

我们可以用wolframalpha观察规律：

以此类推得到：

然后对与：

我们使用wolframalpha编写：

limit (integrate (integrate (u^2-3sin(u-t)^2),t=0 to u),u=0 to x)/(x^8) as x->+∞

可以计算出：

对于第三个，设

求：

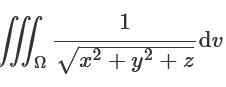
我们需要转换到极坐标求解，设

wolframalpha编写：

(integrate dθ,θ=0 to 2*pi)(integrate r/sqrt(r^2+z) dr, r=0 to sqrt(3z))

integrate 2*pi*sqrt(z) dz, z=1 to 4

计算得到：

最后，三个结果合并为\sqrt[2020]{2020!}-\frac{1}{112}-\frac{28\pi}{3}，md5值即为flag。

2021年

easy_rsa

题目

q= 9961202707366965556741565662110710902919441271996809241009358666778850435448710324711706845973820669201482939820488174382325795134659313309606698334978471
p= 12525187149887628510447403881107442078833803097302579419605689530714690308437476207855511625840027119860834633695330551080761572835309850579517639206740101
c= 28587419802025513525354713621431206010395084854419372005671024739235625817936539010481222419824634956610184430308528941304950093228826213143262329902946812513518444587906469224383320964300417189270202019231856531012143472434842753891213128487132962453421971000901646523331476667655739056951415917218673801225
e = 65537

我的解答：

exp:

import gmpy2
from Crypto.Util.number import long_to_bytes
q= 9961202707366965556741565662110710902919441271996809241009358666778850435448710324711706845973820669201482939820488174382325795134659313309606698334978471
p= 12525187149887628510447403881107442078833803097302579419605689530714690308437476207855511625840027119860834633695330551080761572835309850579517639206740101
c= 28587419802025513525354713621431206010395084854419372005671024739235625817936539010481222419824634956610184430308528941304950093228826213143262329902946812513518444587906469224383320964300417189270202019231856531012143472434842753891213128487132962453421971000901646523331476667655739056951415917218673801225
e = 65537
n = p*q
phi = (p-1) * (q-1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
#UNCTF{Th1s_1s_f1ag_f0r_unctf_2021!!}

探秘中世纪城堡

贝拉在参观一个中世纪的古堡时，在桌上看到了一串一奇怪的字符和描述。你能帮大聪明破解皇珈骑士留下来的谜团吗？

年轻的大帝率领着64位皇珈骑士冲破了双重阻栏夺下了城池。
AZSLh2OofBA0C2qzi25mg2KsYqW7iCSdDq9aBLKsDBWyi259

我的解答：

根据题目提示64代表base64，双重代表栅栏密码，栏数为2，还有凯撒加密

凯撒加密偏移21得到

VUNGc2JjaWV0X2lud25hb2FnTlR7dXNyYl9vWGFnYWRtd259

base64解码得到

UCFsbciet_inwnaoagNT{usrb_oXagadmwn}

栏栅解码

UNCTF{subscribe_to_Xiangwandamowang}

分析badusb流量

一日，某企业的安全管理员发现企业中的电脑遭到了badusb的侵害，以下他分离出来的有问题USB流量，而这似乎跟键盘的键位映射有关。

2018 2011 2006 2017 2009 202f 201C 0027 0018 002D 2004 0015 0008 002D 0019 0008 0015 001C 002D 0011 001E 0006 0008 2030

我的解答

前两位20代表大写，00代表小写，后两位为键码，对照写flag。

exp:

f = open('1.txt','r').readlines()
mappings = { 0x04:"A",  0x05:"B",  0x06:"C", 0x07:"D", 0x08:"E", 0x09:"F", 0x0A:"G",  0x0B:"H", 0x0C:"I",  0x0D:"J", 0x0E:"K", 0x0F:"L", 0x10:"M", 0x11:"N",0x12:"O",  0x13:"P", 0x14:"Q", 0x15:"R", 0x16:"S", 0x17:"T", 0x18:"U",0x19:"V", 0x1A:"W", 0x1B:"X", 0x1C:"Y", 0x1D:"Z", 0x1E:"1", 0x1F:"2", 0x20:"3", 0x21:"4", 0x22:"5",  0x23:"6", 0x24:"7", 0x25:"8", 0x26:"9", 0x27:"0", 0x28:"\n", 0x2a:"[DEL]",  0X2B:"    ", 0x2C:" ",  0x2D:"-", 0x2E:"=", 0x2F:"[",  0x30:"]",  0x31:"\\", 0x32:"~", 0x33:";",  0x34:"'", 0x36:",",  0x37:"." }
for i in range(len(f)):
    num = int(f[i][2:4],16)
    if(f[i][0] == '2'):
        if(num in mappings):
            print(mappings[num].upper(),end='')
    else:
        if (num in mappings):
            print(mappings[num].lower(), end='')
            
            
#output:UNCTF[Y0u-Are-very-n1ce]

UNCTF{Y0u-Are-very-n1ce}

baby_rsa

import gmpy2
import libnum
import random
import uuid
flag="unctf{"+str(uuid.uuid4())+"}"
m=libnum.s2n(flag)

p=libnum.generate_prime(1024)
q=libnum.generate_prime(1024)
n=p*q
e=65537
c=pow(m*p+n,e,n)
print("n=",n)
print("c=",c)
print("e=",e)
#n= 27023180567533176673625876001733765250439008888496677405372613659387969480500400831799338479404533734632060401129194207025095826786316107611502577395964365591899893794206238112244571942694129959717225168573059987542436467778426312967832431595178558711258027999897974942046398583397445299861338203860420721585460676138091828032223153425728023656897880166788811969523526091221520293020106530587453637600349533427641518473788620430866128331962450325767202417824455886116760280239705754222948387172102353564657340216229891342124971948458724351338597649821310431397426705701275774039588035776573373417654649168810548916141
#c= 3489599657527403893851973553294684608504140532554562294027722218597464669848608337663997115805201027340092733823019661706872544231209523772845492398492677185660213963118144668038183924970370481476141221609706208064428560732214361469135212057355342825193598971775551833240699393482839422273480793244841531126642199202744610656153155545415859410361595564197685655133074582118230993519133935533313364233668337427608419528430102794052261190930670933657287272452581248934890029409559234507626012423255430699687038808658327174609660874748540185589263800447650242593224189976058739054174360024536594384447518687126891675059
#e= 65537

我的解答：

考点：dp泄露

exp:

import gmpy2
import libnum
n= 27023180567533176673625876001733765250439008888496677405372613659387969480500400831799338479404533734632060401129194207025095826786316107611502577395964365591899893794206238112244571942694129959717225168573059987542436467778426312967832431595178558711258027999897974942046398583397445299861338203860420721585460676138091828032223153425728023656897880166788811969523526091221520293020106530587453637600349533427641518473788620430866128331962450325767202417824455886116760280239705754222948387172102353564657340216229891342124971948458724351338597649821310431397426705701275774039588035776573373417654649168810548916141
c= 3489599657527403893851973553294684608504140532554562294027722218597464669848608337663997115805201027340092733823019661706872544231209523772845492398492677185660213963118144668038183924970370481476141221609706208064428560732214361469135212057355342825193598971775551833240699393482839422273480793244841531126642199202744610656153155545415859410361595564197685655133074582118230993519133935533313364233668337427608419528430102794052261190930670933657287272452581248934890029409559234507626012423255430699687038808658327174609660874748540185589263800447650242593224189976058739054174360024536594384447518687126891675059
e= 65537
p = gmpy2.gcd(n,c)
q = n//p
phi = (q-1)*(p-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
print(libnum.n2s(int(m//p)))
#unctf{rsa_s1mp1e_0kk}

电信诈骗pro

朕是秦始皇，其实朕没有死，朕在西安兵马俑第四个坑第七排，朕是吃了长生不老药的，朕告诉你啊，朕在陕西有3000吨黄金和300万秦兵被封印，现在只需要30元就能解封，只要你打钱给朕，朕明天直接带部队复活，让你统领三军!建立像古罗马一样的帝国，君无戏言！朕的账户是5.#4&;Sw)2Ti%*Sj1eUU9kTwi*Sj)1S"a8S0)6x-8(x7=

flag格式为unctf{}

我的解答：

ROT47

相减发现和unctf相差64

2022年

md5-1

爆破可见字符得到md5表，再依次遍历密文取出相应字符。

from hashlib import md5

c = '''4c614360da93c0a041b22e537de151eb
8d9c307cb7f3c4a32822a51922d1ceaa
0d61f8370cad1d412f80b84d143e1257
b9ece18c950afbfa6b0fdbfa4ff731d3
800618943025315f869e4e1f09471012
f95b70fdc3088560732a5ac135644506
e1671797c52e15f763380b45e841ec32
c9f0f895fb98ab9159f51fd0297e236d
a87ff679a2f3e71d9181a67b7542122c
8fa14cdd754f91cc6554c9e71929cce7
e1671797c52e15f763380b45e841ec32
8277e0910d750195b448797616e091ad
cfcd208495d565ef66e7dff9f98764da
c81e728d9d4c2f636f067f89cc14862c
c9f0f895fb98ab9159f51fd0297e236d
92eb5ffee6ae2fec3ad71c777531578f
45c48cce2e2d7fbdea1afc51c7c6ad26
cfcd208495d565ef66e7dff9f98764da
a87ff679a2f3e71d9181a67b7542122c
1679091c5a880faf6fb5e6087eb1b2dc
8fa14cdd754f91cc6554c9e71929cce7
4a8a08f09d37b73795649038408b5f33
cfcd208495d565ef66e7dff9f98764da
e1671797c52e15f763380b45e841ec32
c9f0f895fb98ab9159f51fd0297e236d
8fa14cdd754f91cc6554c9e71929cce7
cfcd208495d565ef66e7dff9f98764da
c9f0f895fb98ab9159f51fd0297e236d
cfcd208495d565ef66e7dff9f98764da
e1671797c52e15f763380b45e841ec32
45c48cce2e2d7fbdea1afc51c7c6ad26
1679091c5a880faf6fb5e6087eb1b2dc
e1671797c52e15f763380b45e841ec32
8f14e45fceea167a5a36dedd4bea2543
c81e728d9d4c2f636f067f89cc14862c
c4ca4238a0b923820dcc509a6f75849b
c9f0f895fb98ab9159f51fd0297e236d
a87ff679a2f3e71d9181a67b7542122c
cbb184dd8e05c9709e5dcaedaa0495cf'''.split('\n')

s = list(range(32,127))
t = {}

for k in s:
    t[md5(chr(k).encode()).hexdigest()] = chr(k)

flag=''
for k in c:
    flag += t[k]

print(flag)
# UNCTF{e84fed028b9046fc0e8f080e96e72184}

dddd

题目

110/01/0101/0/1101/0000100/0100/11110/111/110010/0/1111/10000/111/110010/1000/110/111/0/110010/00/00000/101/111/1/0000010

我的解答

1换为 .，0换为 -，摩斯密码解密得：UNCTF{Y4S_TH1S_JUST_M0RSE}。

caesar

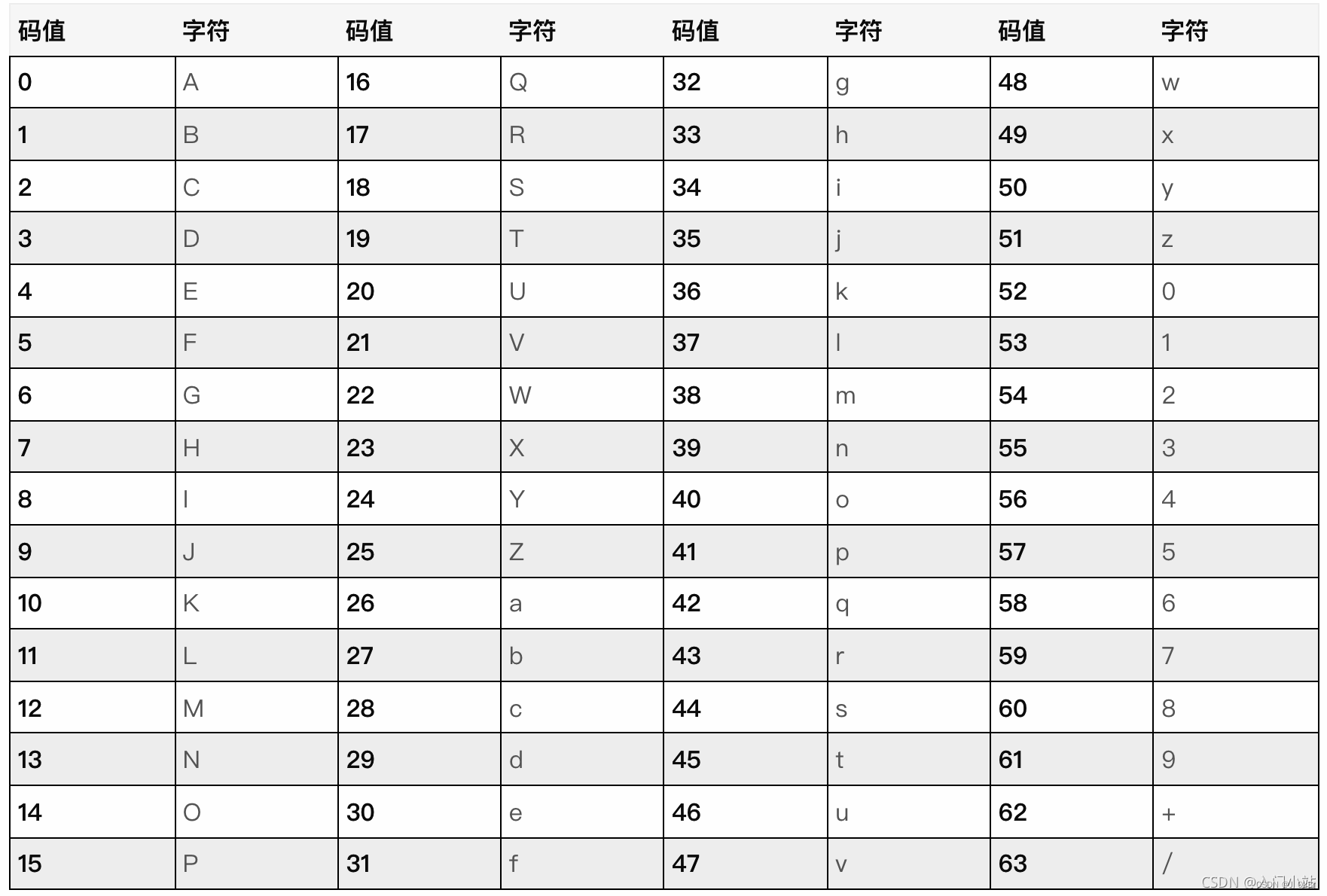
对照base64的表

B6vAy—UNCTF

B-U=1-20(增加了19)

6-N=58-13(减少了45)

以此类推后面3个字母发现，当字母表值小于19时，就加上19，大于45时就减去45

最终得到

UNCTF{w0w_Th1s_d1fFerent_c4eSar}

exp:

import string

s = 'B6vAy{dhd_AOiZ_KiMyLYLUa_JlL/HY_}'
dic = string.ascii_uppercase+string.ascii_lowercase+string.digits+'+/'
print(dic)

d = ord('U')-ord('B')

t = ''
for i in range(len(s)):
  if s[i] == '{' or s[i] == '}' or s[i] == '_':
    t += s[i]
  else:
    t += dic[(dic.index(s[i])+d)%64]

print(t)

# UNCTF{w0w_Th1s_d1fFerent_c4eSar_}

md5-2

比md5-1多了一层异或操作，还原即可。

from hashlib import md5

c = '''4c614360da93c0a041b22e537de151eb
c1fd731c6d60040369908b4a5f309f41
80fdc84bbb5ed9e207a21d5436efdcfd
b48d19bb99a7e6bb448f63b75bc92384
39eaf918a52fcaa5ed9195e546b021c1
795d6869f32db43ff5b414de3c235514
f59a054403f933c842e9c3235c136367
c80b37816048952a3c0fc9780602a2fa
810ecef68e945c3fe7d6accba8b329bd
cad06891e0c769c7b02c228c8c2c8865
470a96d253a639193530a15487fea36f
470a96d253a639193530a15487fea36f
4bdea6676e5335f857fa8e47249fa1d8
810ecef68e945c3fe7d6accba8b329bd
edbb7ab78cde98a07b9b5a2ab284bf0a
44b43e07e9af05e3b9b129a287e5a8df
a641c08ed66b55c9bd541fe1b22ce5c0
abed1f675819a2c0f65c9b7da8cab301
738c486923803a1b59ef17329d70bbbd
7e209780adf2cd1212e793ae8796ed7c
a641c08ed66b55c9bd541fe1b22ce5c0
a641c08ed66b55c9bd541fe1b22ce5c0
636a84a33e1373324d64463eeb8e7614
6ec65b4ab061843b066cc2a2f16820d5
a4a39b59eb036a4a8922f7142f874114
8c34745bd5b5d42cb3efe381eeb88e4b
5b1ba76b1d36847d632203a75c4f74e2
d861570e7b9998dbafb38c4f35ba08bc
464b7d495dc6019fa4a709da29fc7952
8eb69528cd84b73d858be0947f97b7cc
dd6ac4c783a9059d11cb0910fc95d4a
4b6b0ee5d5f6b24e6898997d765c487c
b0762bc356c466d6b2b8f6396f2e041
8547287408e2d2d8f3834fc1b90c3be9
82947a7d007b9854fa62efb18c9fd91f
8ddafe43b36150de851c83d80bd22b0a
c7b36c5f23587e285e528527d1263c8b
2a0816e8af86e68825c9df0d63a28381
63ce72a42cf62e6d0fdc6c96df4687e3'''.split('\n')

cc = [int(k,16) for k in c]
for i in range(1,len(cc)):
    cc[i] ^= cc[i-1]
    
cc = [hex(k)[2:].rjust(32,'0') for k in cc]
print(cc)

s=list(range(32,127))
t={}

for k in s:
    t[md5(chr(k).encode()).hexdigest()]=chr(k)

flag = ''
for k in cc:
    flag += t[k]

print(flag)

# UNCTF{a197271943ceb3c3fe98bcadf10c29d4}

ezRSA

import libnum

p=libnum.generate_prime(256)
e=65537
m=flag

m=libnum.s2n(m)
n=p**4
phi_n=p**4-p**3
d=libnum.invmod(e,phi_n)
c=pow(m,e,n)

print ("n=",n)
print ("e=",e)
print ("c=",c)
62927872600012424750752897921698090776534304875632744929068546073325488283530025400224435562694273281157865037525456502678901681910303434689364320018805568710613581859910858077737519009451023667409223317546843268613019139524821964086036781112269486089069810631981766346242114671167202613483097500263981460561
65537 56959646997081238078544634686875547709710666590620774134883288258992627876759606112717080946141796037573409168410595417635905762691247827322319628226051756406843950023290877673732151483843276348210800329658896558968868729658727981445607937645264850938932045242425625625685274204668013600475330284378427177504

我的解答：

import gmpy2
n = 62927872600012424750752897921698090776534304875632744929068546073325488283530025400224435562694273281157865037525456502678901681910303434689364320018805568710613581859910858077737519009451023667409223317546843268613019139524821964086036781112269486089069810631981766346242114671167202613483097500263981460561
e = 65537
c = 56959646997081238078544634686875547709710666590620774134883288258992627876759606112717080946141796037573409168410595417635905762691247827322319628226051756406843950023290877673732151483843276348210800329658896558968868729658727981445607937645264850938932045242425625625685274204668013600475330284378427177504
p = gmpy2.iroot(n,4)[0]
f = p**3*(p-1)
d = gmpy2.invert(e,f)
m = pow(c,d,n)
print(bytes.fromhex(hex(m)[2:]))
# b'unctf{pneum0n0ultram01cr0sc0p01cs01l01c0v0lcan0c0n010s01s}'

Single table

根据题目:单表置换，按照所给例子的规律，我们排出来一个表

然后每两个字母一组，取表上两个字母分别为原点的坐标系的交点的字母来代换原字母可得到：

UNCTF{GODY_OUK_NOWP_LAYFAIRX}

格式整理一下：

UNCTF{GOD_YOU_KNOW_PLAYFAIR}

Multi table

变表维吉尼亚密码，先根据前4字符确定key值，再遍历爆破。

from string import ascii_uppercase

base_table = ['J', 'X', 'I', 'S', 'E', 'C', 'R', 'Z', 'L', 'U', 'K', 'Q', 'Y', 'F', 'N', 'V', 'T', 'P', 'O', 'G', 'A', 'H', 'D', 'W', 'M', 'B']

table={}
for i in range(26):
  table[i]=ascii_uppercase[i:]+ascii_uppercase[:i]

ori = 'UNCT'
res = 'SDCG'
key = []

for i in range(4):
  for k,v in table.items():
    if v[base_table.index(ori[i])] == res[i]:
      key.append(k)
      break

print(key)

c = 'SDCGW{MPN_VHG_AXHU_GERA_SM_EZJNDBWN_UZHETD}'
flag = ''
x = 0
for i in range(len(c)):
  if c[i] in ascii_uppercase:
    now = table[key[x%4]].index(c[i]) 
    flag += base_table[now]
    x += 1
  else:
    flag += c[i]

print(flag)

# [9, 15, 23, 16]
# UNCTF{WOW_YOU_KNOW_THIS_IS_VIGENERE_CIPHER}

babyRSA

m高位泄露的Coppersmith攻击。

n = 25300208242652033869357280793502260197802939233346996226883788604545558438230715925485481688339916461848731740856670110424196191302689278983802917678262166845981990182434653654812540700781253868833088711482330886156960638711299829638134615325986782943291329606045839979194068955235982564452293191151071585886524229637518411736363501546694935414687215258794960353854781449161486836502248831218800242916663993123670693362478526606712579426928338181399677807135748947635964798646637084128123883297026488246883131504115767135194084734055003319452874635426942328780711915045004051281014237034453559205703278666394594859431
c = 15389131311613415508844800295995106612022857692638905315980807050073537858857382728502142593301948048526944852089897832340601736781274204934578234672687680891154129252310634024554953799372265540740024915758647812906647109145094613323994058214703558717685930611371268247121960817195616837374076510986260112469914106674815925870074479182677673812235207989739299394932338770220225876070379594440075936962171457771508488819923640530653348409795232033076502186643651814610524674332768511598378284643889355772457510928898105838034556943949348749710675195450422905795881113409243269822988828033666560697512875266617885514107
e =  6 
mbar = 11941439146252171444944646015445273361862078914338385912062672317789429687879409370001983412365416202240
kbits = 60
nbits = n.nbits()
print("upper {} bits of {} bits is given".format(nbits - kbits, nbits))
PR.<x> = PolynomialRing(Zmod(n))
f = (mbar + x)^e - c
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]  # find root < 2^kbits with factor = n
m = mbar + x0
print(bytes.fromhex(hex(m)[2:]))

# b'UNCTF{27a0aac7-76cb-427d-9129-1476360d5d1b}'

easy_RSA

题目

from Crypto.Util.number import *
from gmpy2 import *
from secret import flag
import random
assert flag.startwith(b"flag{")
e=0x10001
c=6423951485971717307108570552094997465421668596714747882611104648100280293836248438862138501051894952826415798421772671979484920170142688929362334687355938148152419374972520025565722001651499172379146648678015238649772132040797315727334900549828142714418998609658177831830859143752082569051539601438562078140 
n=102089505560145732952560057865678579074090718982870849595040014068558983876754569662426938164259194050988665149701199828937293560615459891835879217321525050181965009152805251750575379985145711513607266950522285677715896102978770698240713690402491267904700928211276700602995935839857781256403655222855599880553
 
m=bytes_to_long(flag)
p=getprime(512)
q=getprime(512)
n=p*q
c=pow(m,e,n)
print("n={}".format(n))
print("c={}".format(c))
tmp=random.randint(100,300)   #生成从100-300的随机数
print("p>>tmp={}".format(p>>tmp))
 
#c=6423951485971717307108570552094997465421668596714747882611104648100280293836248438862138501051894952826415798421772671979484920170142688929362334687355938148152419374972520025565722001651499172379146648678015238649772132040797315727334900549828142714418998609658177831830859143752082569051539601438562078140 
 
#n=102089505560145732952560057865678579074090718982870849595040014068558983876754569662426938164259194050988665149701199828937293560615459891835879217321525050181965009152805251750575379985145711513607266950522285677715896102978770698240713690402491267904700928211276700602995935839857781256403655222855599880553
 
#p>>200=8183408885924573625481737168030555426876736448015512229437332241283388177166503450163622041857

p高位泄露的Coppersmith攻击。

c = 6423951485971717307108570552094997465421668596714747882611104648100280293836248438862138501051894952826415798421772671979484920170142688929362334687355938148152419374972520025565722001651499172379146648678015238649772132040797315727334900549828142714418998609658177831830859143752082569051539601438562078140
n = 102089505560145732952560057865678579074090718982870849595040014068558983876754569662426938164259194050988665149701199828937293560615459891835879217321525050181965009152805251750575379985145711513607266950522285677715896102978770698240713690402491267904700928211276700602995935839857781256403655222855599880553
p4 = 8183408885924573625481737168030555426876736448015512229437332241283388177166503450163622041857
e =  0x10001
pbits = 512
kbits = 200
print(p4.nbits())
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
p = p4+int(roots[0]) 
q = n//p
f = (p-1)*(q-1)
d = inverse_mod(e,f)
m = pow(c,d,n)
print(bytes.fromhex(hex(m)[2:]))
# flag{It is a very_intersting_test!!!}

今晚吃什么

全部大写

10000 换 A，00000 换 B，培根密码解得 CRYPROISFUN

Today_is_Thursday_V_me_50

按代码逻辑还原即可。

import random
import itertools
from Crypto.Util.number import *
from Crypto.Util.strxor import strxor

name = "unctf"
key1 = b'Today_is_Thursday_V_me_50'
key1_num = bytes_to_long(key1)

c = b'Q\x19)T\x18\x1b(\x03\t^c\x08QiF>Py\x124DNg3P'

random.seed(key1_num)
message = b''
for i in c:
    temp_num = random.randint(1,128)
    message += long_to_bytes(temp_num ^ i)

guess = [i for i in itertools.permutations(name, 5)]

for i in range(4):
    what = guess.pop(50)

name = ''.join(j for j in what)
mask = strxor(5*name.encode(),key1)
print(mask)
out = strxor(mask,message)
print(out)

# b'unctf{1_l0ve_Thurs4Ay!!!}'

Fermat

题目

from Crypto.Util.number import *
from gmpy2 import *
 
flag=b'UNCTF{}'
e=0x10001
p=getPrime(1024)
q=getPrime(1024)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
x=getPrime(1024)
assert gift+x==x*p
print(n)
print(c)
print(gift)
 
# 19793392713544070457027688479915778034777978273001720422783377164900114996244094242708846944654400975309197274029725271852278868848866055341793968628630614866044892220651519906766987523723167772766264471738575578352385622923984300236873960423976260016266837752686791744352546924090533029391012155478169775768669029210298020072732213084681874537570149819864200486326715202569620771301183541168920293383480995205295027880564610382830236168192045808503329671954996275913950214212865497595508488636836591923116671959919150665452149128370999053882832187730559499602328396445739728918488554797208524455601679374538090229259
# 388040015421654529602726530745444492795380886347450760542380535829893454552342509717706633524047462519852647123869277281803838546899812555054346458364202308821287717358321436303133564356740604738982100359999571338136343563820284214462840345638397346674622692956703291932399421179143390021606803873010804742453728454041597734468711112843307879361621434484986414368504648335684946420377995426633388307499467425060702337163601268480035415645840678848175121483351171989659915143104037610965403453400778398233728478485618134227607237718738847749796204570919757202087150892548180370435537346442018275672130416574430694059
# 28493930909416220193248976348190268445371212704486248387964331415565449421099615661533797087163499951763570988748101165456730856835623237735728305577465527656655424601018192421625513978923509191087994899267887557104946667250073139087563975700714392158474439232535598303396614625803120915200062198119177012906806978497977522010955029535460948754300579519507100555238234886672451138350711195210839503633694262246536916073018376588368865238702811391960064511721322374269804663854748971378143510485102611920761475212154163275729116496865922237474172415758170527875090555223562882324599031402831107977696519982548567367160

我的解答

import gmpy2
from Crypto.Util.number import *
n = 19793392713544070457027688479915778034777978273001720422783377164900114996244094242708846944654400975309197274029725271852278868848866055341793968628630614866044892220651519906766987523723167772766264471738575578352385622923984300236873960423976260016266837752686791744352546924090533029391012155478169775768669029210298020072732213084681874537570149819864200486326715202569620771301183541168920293383480995205295027880564610382830236168192045808503329671954996275913950214212865497595508488636836591923116671959919150665452149128370999053882832187730559499602328396445739728918488554797208524455601679374538090229259
c = 388040015421654529602726530745444492795380886347450760542380535829893454552342509717706633524047462519852647123869277281803838546899812555054346458364202308821287717358321436303133564356740604738982100359999571338136343563820284214462840345638397346674622692956703291932399421179143390021606803873010804742453728454041597734468711112843307879361621434484986414368504648335684946420377995426633388307499467425060702337163601268480035415645840678848175121483351171989659915143104037610965403453400778398233728478485618134227607237718738847749796204570919757202087150892548180370435537346442018275672130416574430694059
g = 28493930909416220193248976348190268445371212704486248387964331415565449421099615661533797087163499951763570988748101165456730856835623237735728305577465527656655424601018192421625513978923509191087994899267887557104946667250073139087563975700714392158474439232535598303396614625803120915200062198119177012906806978497977522010955029535460948754300579519507100555238234886672451138350711195210839503633694262246536916073018376588368865238702811391960064511721322374269804663854748971378143510485102611920761475212154163275729116496865922237474172415758170527875090555223562882324599031402831107977696519982548567367160
e = 0x10001

p = gmpy2.gcd(pow(2,g,n)-1,n)
q = n//p
f = (p-1)*(q-1)
d = gmpy2.invert(e,f)
m = pow(c,d,n)
print(long_to_bytes(m))
# b'UNCTF{DO_y0u_Fermat_1ittle_theOrem}'

超级加倍

小e

import gmpy2
c=364948328635256862807658970246807356738683637564484151183420122283833769442806688034764747801289594899501872549412387392353830842750341246881725380294423193634163908298756097744423833369487321345708403908358587818931161805853745707954962941881920962518131654701890269025702523666873057795301975752113492236398361724355733200822450695761
m=gmpy2.iroot(c,4)[0]
print(bytes.fromhex(hex(m)[2:]))

# b'flag{it_is_much_bigger_than_before}'

EZcry

提示1：流密码

密文：dd9f58b37289edc2c40133ab9f0439c140aafe7cfd501f8c3d79b1856c9bda598ce34a02a57c，

key：12345678

RC4成功解出 flag{83e429d991d24c548b9dbd256975d0d5}

2020年

easy_rsa

鞍山大法官开庭之缺的营养这一块怎么补

简单的RSA

wing

signin

快乐数学_0x00

2021年

easy_rsa

探秘中世纪城堡

分析badusb流量

baby_rsa

电信诈骗pro

2022年

md5-1

dddd

caesar

md5-2

ezRSA

Single table

Multi table

babyRSA

easy_RSA

今晚吃什么

Today_is_Thursday_V_me_50

Fermat

超级加倍

EZcry