命题逻辑那些事 | 2. 主析(合)取范式
一、必要概念
简单X取式
简单析取式、简单合取式,说白了就是不知道这个简单是个啥?
简单就是有限
你可以说是公式的长度有限,或者公式包含的命题变项有限,反正就是有限
当然,还都得是析(合)取联结词
这个概念有啥用吗?大抵是没啥用罢。
X取范式
析取范式、合取范式,这个范,又从何说起?
打个比方:
这就是个析取范式,( )里都是简单合取式,再通过析取符号连接起来
由有限个 简单合取式 组成的析取式,就是析取范式 (没错,又是有限)
合取范式同理
主X取范式、极小(大)项
这是激动人心的一步!步入正题了!
首先,主析取范式 比 析取范式 多了个主,它不同在哪呢?
主析取范式的每个简单合取式中,每个变元都出现了一次。
我们举个例子:
不难看出,在同一个( )内,每个变元都出现了一次
其中
- ( ∧ ∧ ) 是极小项
- ( ∨ ∨ ) 是极大项
记忆法:∧ 是一个不包容的符号,喜欢排斥他人的符号(必须两边都为1才为1,要求很苛刻),因此这个符号越多,包容的越少,故称极小项。
二、主X取范式的性质
1、每个命题公式都有其唯一主析取范式和主合取范式
2、每个命题公式的主析取范式和主合取范式互补
互补是什么?这会引出个很重要的概念
还记得上一篇文章讲到的成真赋值可以用来干嘛吗?
是的,这和角码有关!但角码又是什么?
让我们先从角码开始:
极小项可以用一种方法来表示,那就是小写字母m + 角码
而极小项本身可以转化为一个二进制数,例如:
再将二进制转为十进制数,这个数值即为角码
因此上面的两个极小项就可以表示为
那这和成真赋值又有啥关联呢?让我们顺便插入下一条性质——
3、极小项角码 = 其公式的成真赋值(插入在第2条性质中讲解)
还记得我们说成真赋值是一组数,能让公式最终成真的一组数
这组数自然也是用二进制来表示每个变项的真与假
当然成真赋值可能有很多,那主析取范式也是由多个极小项析取而来的嘛
在书上说,通过成真赋值求主析取范式的方法,是求主析取范式的方法之一。
而我之所以把它搬到性质这里来,是因为我暂时没见到什么例题用过这种方法。
我们讲回第2条性质本身,既然极小项可以表示为小写字母m + 角码
那么极大项自然也可以,极大项可表示为 大写字母M+角码
假设一个公式包含n个变项,那么则有2ⁿ种赋值,即2ⁿ个角码
其中一部分属于极小项,另一部分用于极大项
因此我们说主析取范式和主合取范式互补的意思就是说:
额……举个栗子吧,
对于一个有3个变项的公式来说,假如主析取范式为
则此公式的主合取范式即为
根据以上,我们也不难得出极大项角码 = 其公式的成真赋值的反码
三、求主析取范式
我们既然知道了主析取范式和主合取范式是互补的,那么我们还需要求出其中之一即可
我们可以先大致根据原式的"形状"选择出 求哪个更方便一些
不如直接来道例题吧!
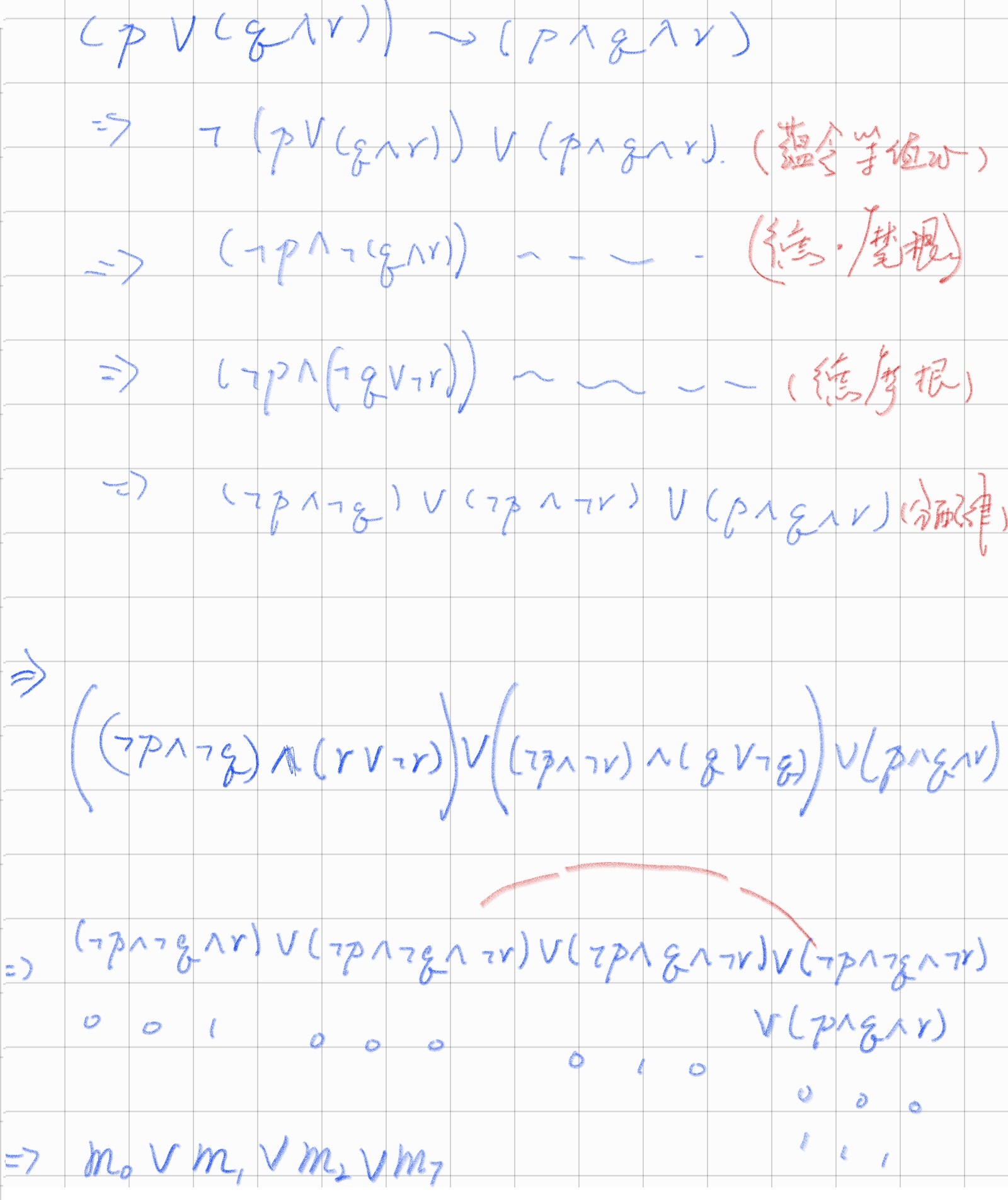
我们能看出前面都是一些正常的演算,
其实第一步已经展示出了一些主析取范式的雏形,即从这里开始我决定先求主析取范式
演算到分配律那一行时是一个重要的转折点
从这里开始主析取范式的框架已经完成,接下来要做的就是硬往里填充,让简单合取式被喂养成极小项,也就是让每一个( )里都包括所有变项
这里有一个很重要的东西 ——怎么塞?
要主析,括号里的就是析取;要主合,括号里的就是合取
话不多说,看图!
