线性dp:大盗阿福(打家劫舍)
大盗阿福
- 本题与leetcode198题——打家劫舍的题意一模一样,阅读完本文以后可以尝试以下题目
题目叙述:
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。这条街上一共有N家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。作为一向谨慎作案的大盗阿福不愿意冒着被警察追捕的风险行窃。他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
- 输入的第一行是一个整数T,表示一共有T组数据。
- 接下来的每组数据,第一行是一个整数N,表示一有N家店铺。
- 第二行是N个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过1000。
输出格式
- 对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
输入样例:
2
3
1 8 2
4
10 7 6 14
输出样例:
8
24
样例解释:
- 对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。对于第二组样例,阿福选择第1和4家店铺行窃获得的现金数量为10+14=24.
动态规划思路分析
- 设我们打劫的店铺数量为
i,获取的价值和为dp,那么dp明显是i的一个函数,那么我们就用dp[i]作为状态变量,dp[i]表示偷前i家店铺所能获取的价值最大值
状态变量以及它的含义
- 由上面分析可知,我们设立
dp[i]作为状态变量,并且dp[i]的含义是偷前i家店铺所能获取收益的最大值.
递推公式
- 我们设
dp[i],在i的这个位置有两种状态:- 1.第i家店铺不偷——
dp[i]=dp[i-1] - 2.第i家店铺偷——
dp[i]=dp[i-2]+w[i],w[i]为第i家店铺的价值
- 1.第i家店铺不偷——
具体细节如下图所示:
遍历顺序:
- 由上面两步分析可知,
dp[i]的状态一定是由前面dp[i-1],dp[i-2],推出来的,所以说遍历顺序一定是从前向后遍历。
如何初始化?
- 我们首先得处理好边界条件:
dp[0]和dp[1]怎么处理? - 偷前0家店铺的最大价值显然是
0,偷前1家店铺的最大价值显然为w[1] - 处理好边界条件以后,我们再从前向后,依据递推公式进行递推就行了
举例验证dp数组
下标:1,2,3,4
w[i]:10,7,6,14
dp[i]:10,10,16,24
- 通过样例2分析可知,我们的dp数组没有分析错。因此我们验证了我们的dp数组的正确性。
优化
-
我们可以用
dp[i-1]的状态直接推出dp[i]的状态。 -
我们状态表示可以优化成:
f[i][0]表示不偷第i家店铺能获取的最大值f[i][1]表示偷第i家店铺能获取的最大值
-
那么我们的状态转移方程就可以从
dp[i-1]推出,不偷第i家店铺,那么我们就可以偷第i-1家店铺,也可以不偷,我们选取这两个之中的最大值,如果偷第i家店铺的话,第i-1家店铺我们一定只能选择不偷。- 不偷:
dp[i][0]=max(dp[i-1][0],dp[i-1][1]) - 偷:
dp[i][1]=dp[i-1][0]+w[i]
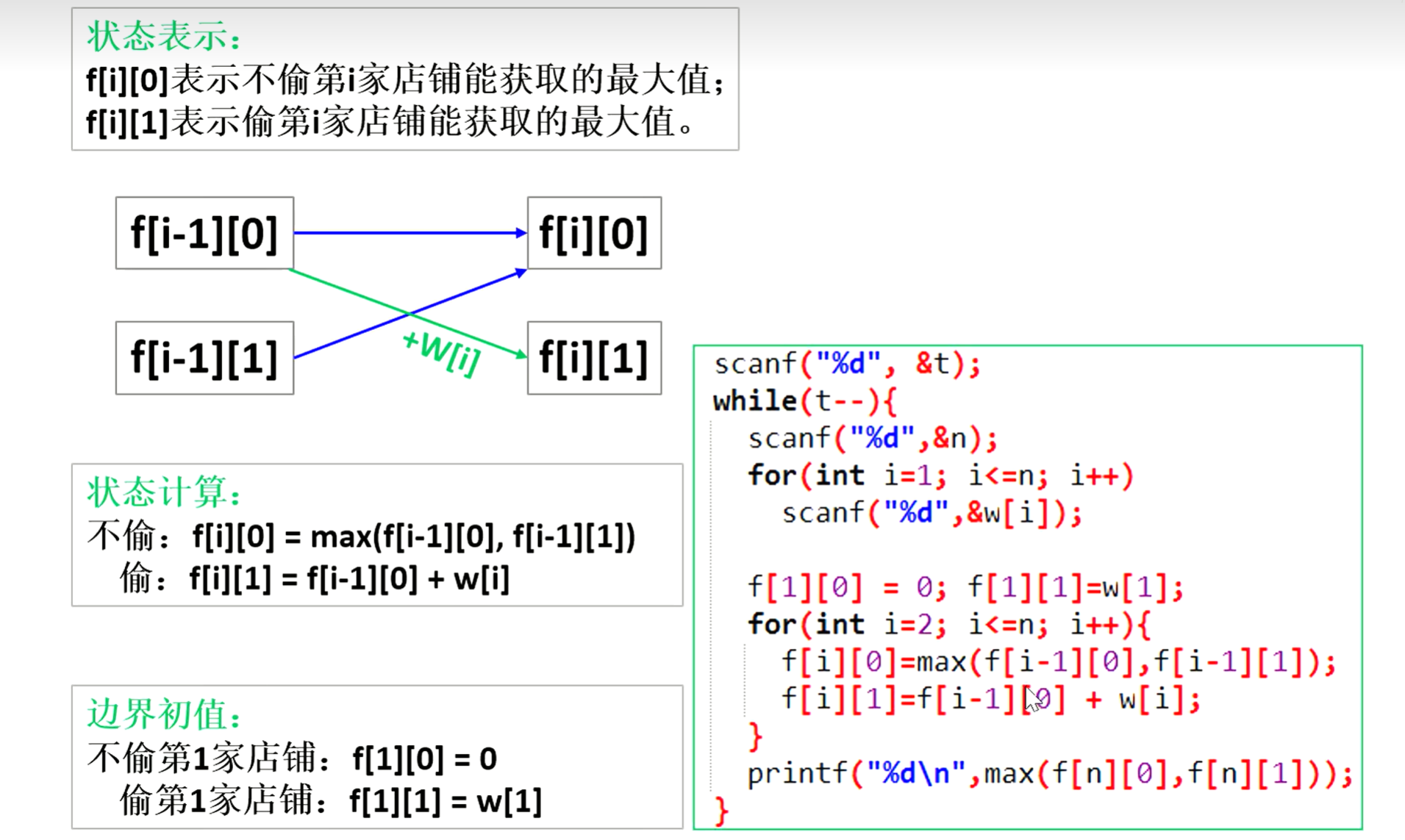
- 不偷:
优化后的边界处理:
- 不偷第1家店铺:
f[i][0]=0 - 偷第1家店铺:
f[i][1]=w[1]
优化后的代码处理:
scanf("%d",&t)
while(t--){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
f[1][0]=0;f[1][1]=w[1];
for(int i=2;i<=n;i++){
f[i][0]=max(f[i-1][0],f[i-1][1]);
f[i][1]=f[i-1][0]+w[i];
}
printf("%d\n",max(f[n][0],f[n][1]));
}
总结:

- 我们上面讲述的两种方法,第一种方法叫做分步转移,第二种方法叫做分类转移,在有些情况下,二者都能使用,而在某些题目当中,只能使用分类转移的方法,我们在以后也会介绍的!希望大家能理解这两种做法。
