并行计算——绪论
一、绪论
1.1 基本概念
- 加速比:表示加速效果。单个处理器运行花费时间 / P个处理器运行花费时间;\(S=\frac{T(1)}{T(p)}\)
- 效率:\(E = \frac{S}{p} = \frac{T(1)}{T(p)\times p}\)
- 开销:\(C=T(p)\times p\)
- 可扩展性:处理器数目增多时并行程序的行为;
- 计算通信比:计算花费时间 / 处理器消息通信花费时间;
- 计算:在1个时间单位内,每个PE(处理单元)能完成2个数相加,并在本地内存保存计算结果;
- 通信:在3个单位时间内,一个PE能够把数据从自己的本地内存发送到另一个PE的本地内存;
- 输入和输出:程序开始时,整个输入数组A保存在0号处理单元PE0,程序结束时,计算结果应汇聚到PE0;
- 同步:所有PE同时进行计算、通信,或处于闲置状态;
1.2 求和案例
1.2.1 分配流程
PE = 1:即为串行。
PE = 2:PE#0分1半任务给PE#1,分别计算,PE#1将求和后数据汇聚到PE#0。

PE = 4:

1.2.2 分发时间计算
以PE = 2为例
- 最初PE#0存储全部数据;
- PE#0发送一般数据给PE#1,花费3个单位时间;(自己规定的,见1.2.4)
- 每个处理单元将数据相加,花费511个单元时间;(因为每个处理器分别有511个数据)
- PE#1求和后数据返回给PE#1,花费3个单元时间;
- PE#0把2部分数据相加,花费1个时间单元;
共计 3 + 511 + 3 + 1 个时间单元
通用表达式
使用\(p=2^{q}\)个处理单元,以及\(n=2^{k}\)个输入整数
- 数据分发次数:\(3 \times q\)
- 本地求和:\(\frac{n}{p} -1 = 2^{k-q}-1\)
- 收集中间数据:\(3 \times q\)
- 中间结果求和::\(q\)
则共 \(T(p,n)=T(2^{q},2^{k})=3q+2^{k-q}-1+3q+q=2^{k-q}-1+7q\)
1.2.3 扩展性分析
强扩展性分析:改变处理器的数量,并行计算时间、加速比、开销和效率变化规律;
弱扩展性分析:改变处理器的数量,同时改变数据量,并行计算时间、加速比、开销和效率变化规律;
上述算法不是强扩展性,是弱扩展性。
1.2.4 一般情形计算
$\alpha $:执行一次单独的假发操作需要的时长
$\beta $:传输一批整数需要的时长;
运行时间:\(T_{\alpha,\beta }(p,n)=T(2^{q},2^{k})=\beta q+\alpha(2^{k-q}-1)+\beta q+\alpha q=2\beta q +\alpha (2^{k-q}-1 + q)\)
加速比:$S_{\alpha ,\beta } (2^{q}, 2^{k})=\frac{T_{\alpha ,\beta }(2^{0}, 2^{k})}{T_{\alpha ,\beta }(2^{q}, 2^{k}) }=\frac{\alpha(2^{k}-1)}{2\beta q + \alpha(2^{k-q}-1+q)} $
通信比:\(\gamma=\frac{\alpha}{\beta}\)
求解最优单元:\(2^{q}={\frac{\gamma\ln2}{2+\gamma}}2^{k}\)
比如,对于\(\gamma=\frac{1}{3},n=1024\),加速比最大可求\(p=1000\)
当处理数据规模固定,并行效率和加速比依赖于计算单元个数和计算通信比;
1.3 并行计算基础
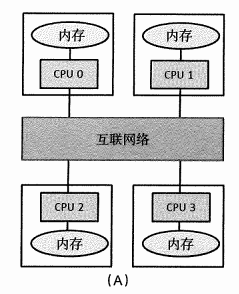
1.3.1 分布式内存
特点:每个PE只能访问自己的本地内存,如果跨PE访问,需要一个显式的通信步骤。
数据划分是分布式内存系统编程的关键。
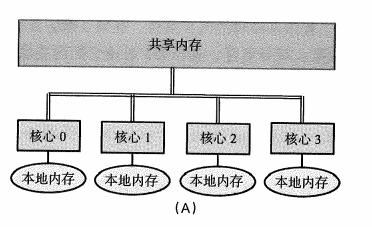
1.3.2 共享内存系统
通过一个共享总线或者纵横交换机,所有的CPU都能访问同一块公共内存空间。
- 除了共享主存外,每个核心包含一块更小的本地内存;
- 缓存一致性,存储在本地缓存中的值和存储在共享内存中的值保持一致;
1.4 并行程序设计考虑因素
- 划分:给定的问题划分为子问题;
- 通信:选定划分方案决定了进程或县城之间需要的通信量和通信类型;
- 同步:为了以正确的方式共同运行,线程或进程之间可能需要同步操作;
- 负载平衡:多个县城或多个进程之间的工作量需要平均分配,以平衡他们各自的负载,并最小化空闲时间;
求和案例

1.5 不同层次的并行
- 节点级并行化:需要针对分布式内存机器的模型实现算法,例如MPI(在第9章深入学习)或者UPC++(在第10章深人学习)等。
- 节点内的并行化:通常基于针对共享内存系统(多核CPU)的语言,比如C++多线程(在第4章深人学习),或者OpenMP(在第6章深人学习)。
- 加速卡级的并行化:把一部分计算任务分配给加速卡承担,比如大规模并行GPU等,借助包括CVDA在内的特定语言(将在第7章深入学习)。

参考:《并行程序设计》